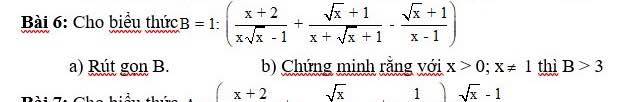a: Ta có: \(B=1:\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{x-1}\right)\)
\(=1:\left(\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x-\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
b.
Bạn phía dưới đã thu gọn được \(B=\frac{x+\sqrt{x}+1}{\sqrt{x}}\)
Áp dụng BĐT Cô-si: $x+1\geq 2\sqrt{x}$
$\Rightarrow x+\sqrt{x}+1\geq 3\sqrt{x}$
$\Rightarrow B=\frac{x+\sqrt{x}+1}{\sqrt{x}}\geq 3$
Dấu "=" xảy ra khi $x=1$. Mà $x\neq 1$ nên dấu $=$ không xảy ra. Do đó $B>3$
Ta có đpcm.