\(\dfrac{ay-bx}{c}=\dfrac{cx-az}{b}=\dfrac{bz-cy}{a}\\ \Rightarrow\dfrac{acy-bcx}{c^2}=\dfrac{bcx-abz}{b^2}=\dfrac{abz-acy}{a^2}=\dfrac{acy-bcx+bxc-abz+abz-acy}{a^2+b^2+c^2}=0\\ \Rightarrow\left\{{}\begin{matrix}ay-bx=0\\cx-az=0\\bz-cy=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}ay=bx\\cx=az\\bz=cy\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{a}=\dfrac{y}{b}\\\dfrac{x}{a}=\dfrac{z}{c}\\\dfrac{y}{b}=\dfrac{z}{c}\end{matrix}\right.\\ \Rightarrow\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\)
Đại số lớp 7
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
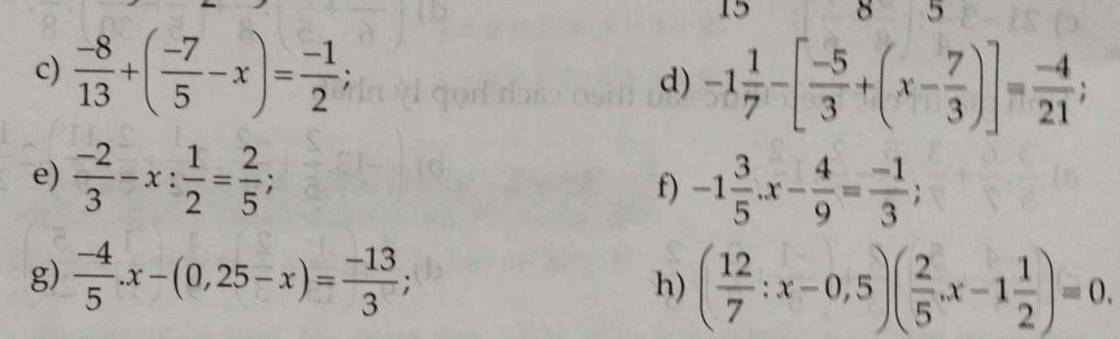 Giúp em với ạ , em đang cần gấp . Em cảm ơn ạ ! =.=
Giúp em với ạ , em đang cần gấp . Em cảm ơn ạ ! =.=

Giúp em với ạ bài khó quá không làm được . Em cảm ơn ạ !
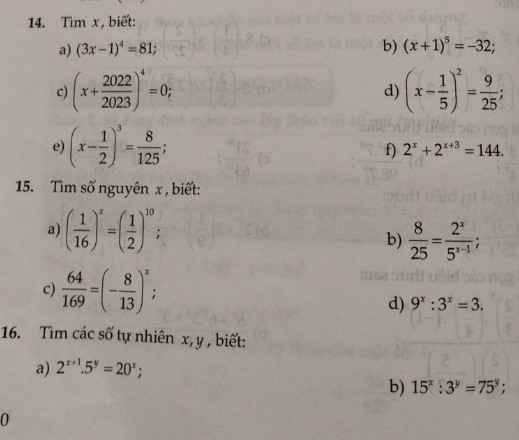
Giúp em với , em cảm ơn nhiều ạ .
Giúp em với ạ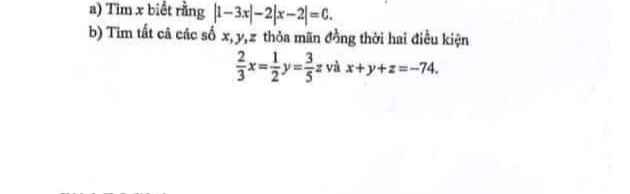
Giúp em với ạ
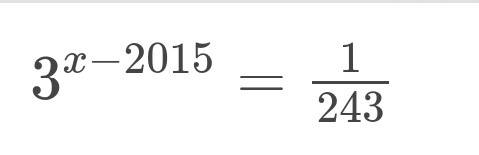 giúp em với ạ
giúp em với ạ
Giúp em bài 4.13 với ạ. Em cảm ơn nhiều 
ANH CHỊ ƠI GIÚP EM 2 BÀI TOÁN LỚP 7 VỚI Ạ .MAI EM KIỂM TRA GIỮA KÌ RỒI .EM CẢM ƠN RẤT NHIỀU Ạ.
Làm giúp em câu 3 với ạ , em đang cần gấp 

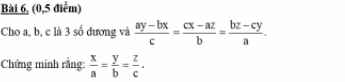 Giúp em với ạ
Giúp em với ạ







