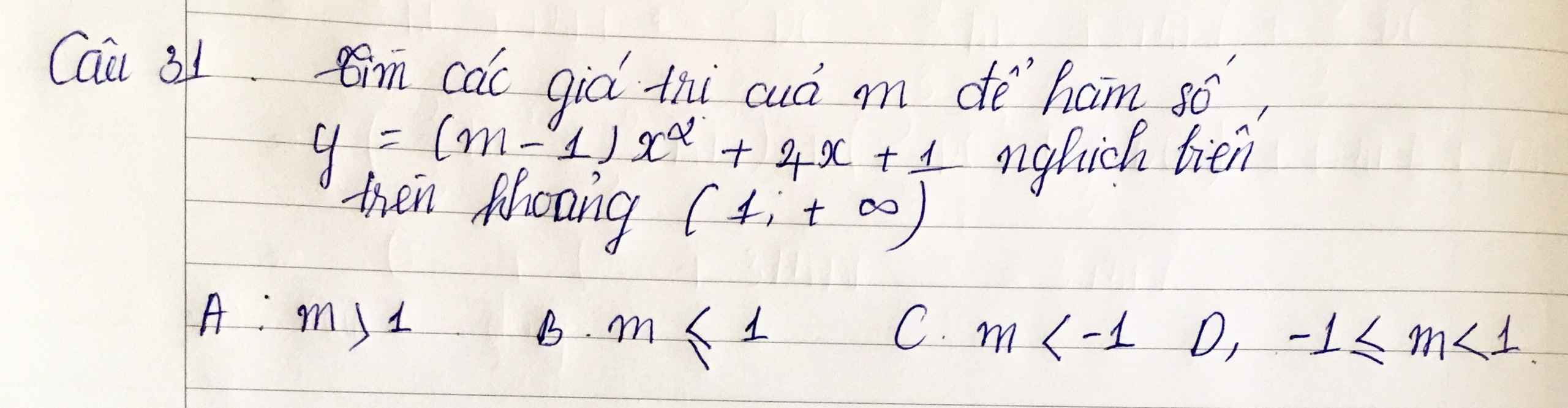Lời giải:
Hàm số nghịch biến trên $(1;+\infty)$ khi:
$y'=2(m-1)x+4\leq 0, \forall x\in (1;+\infty)$
$\Leftrightarrow m-1\leq \frac{-2}{x}, \forall x\in (1;+\infty)$
$\Leftrightarrow m-1\leq (\frac{-2}{x})_{\min}, \forall x\in (1;+\infty)$
$\Rightarrow m-1\leq -2$
$\Leftrightarrow m\leq -1$
Đáp án C.
Đúng 2
Bình luận (0)