a)Có `hat{SAB}=hat{ACB}`(2 góc nt và góc tạo bởi tia tiếp tuyến cùng chắn 1 cung)
Xét tam giác SAB và tam giác SCA ta có:
`hat{SAB}=hat{SCA}(CMT)`
`hat{ASC}` chung
`=>Delta SAB~ Delta SCA`
`=>(SA)/(SB)=(SC)/(SA)`
`=>SA^2=SB.SC`
Xét (O) có:
M là tđ BC
`=>OM bot BC`
`=>hat{OMB}=90^o`
Xét tg SAOM có:
`hat{SAO}+hat{SMO}=180^o`
`=>` tg SAOM nt
b) Ta có: \(OC^2=OA^2=OH.OS\Rightarrow\dfrac{OC}{OH}=\dfrac{OS}{OC}\)
Xét \(\Delta OCH\) và \(\Delta OSC:\) Ta có: \(\left\{{}\begin{matrix}\angle COSchung\\\dfrac{OC}{OH}=\dfrac{OS}{OC}\end{matrix}\right.\)
\(\Rightarrow\Delta OCH\sim\Delta OSC\left(c-g-c\right)\)








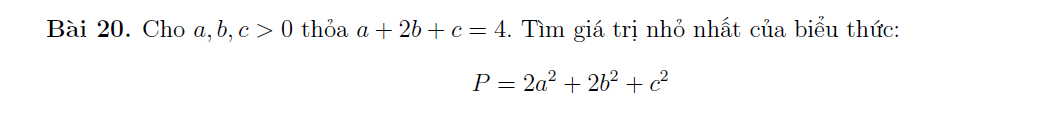

 Mọi người ơi,giúp em bài với ạ em cảm ơn ạ
Mọi người ơi,giúp em bài với ạ em cảm ơn ạ