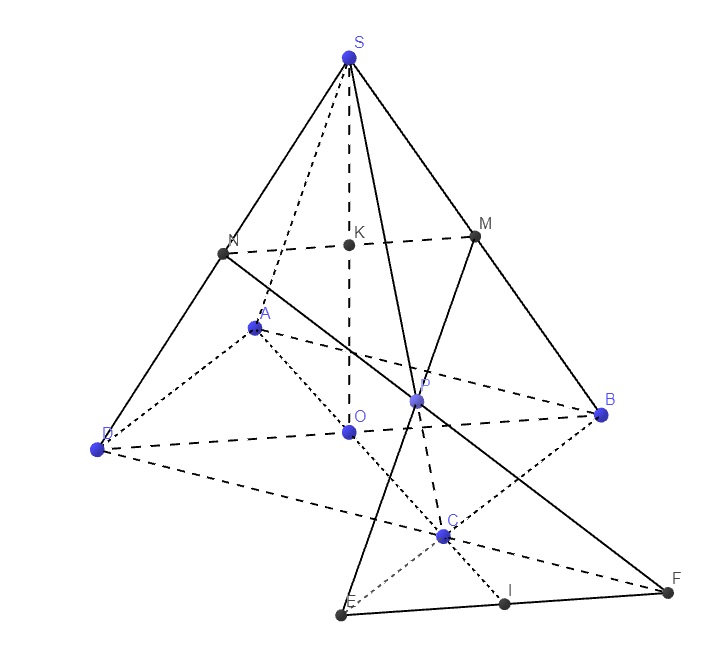
a.
Do \(SP>PC\) nên MP ko song song BC và NP không song song CD
Trong mp (SBC), nối MP kéo dài cắt BC tại E
Trong mp (SCD), nối NP kéo dài cắt CD tại F
\(\Rightarrow\left\{{}\begin{matrix}E\in\left(MNP\right)\cap\left(ABCD\right)\\F\in\left(MNP\right)\cap\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow EF=\left(MNP\right)\cap\left(ABCD\right)\)
b.
\(O=AC\cap BD\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Trong mp (SBD), nối MN cắt SO tại K
\(\left\{{}\begin{matrix}K\in MN\in\left(MNP\right)\\K\in SO\end{matrix}\right.\) \(\Rightarrow K=SO\cap\left(MNP\right)\) (1)
c.
Do \(\left(CAD\right)\equiv\left(ABCD\right)\) (hai mp có 3 điểm chung là A, C, D)
\(\Rightarrow EF=\left(CAD\right)\cap\left(MNP\right)\)
(Tại sao người ta lại cho câu này khi đã có câu a nhỉ?)
d.
\(K\in SO\in\left(SAC\right)\) (2)
(1);(2) \(\Rightarrow K\in\left(MNP\right)\cap\left(SAC\right)\) (3)
\(\left\{{}\begin{matrix}P\in\left(MNP\right)\\P\in SA\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow P\in\left(SAC\right)\cap\left(MNP\right)\) (4)
\(\left\{{}\begin{matrix}I\in EF\in\left(MNP\right)\\I\in AC\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow I\in\left(MNP\right)\cap\left(SAC\right)\) (5)
(3);(4);(5) \(\Rightarrow K,I,P\) cùng nằm trên giao tuyến của ((MNP) và (SAC)
Hay K, I, P thẳng hàng












 Giúp e vs ạ
Giúp e vs ạ


