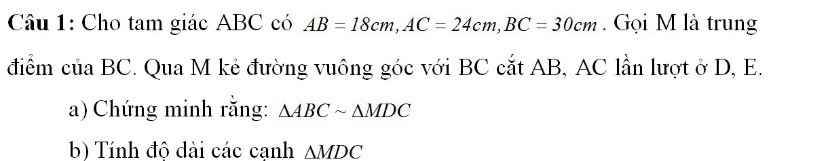
a) Ta có:
\(AB^2+AC^2=18^2+24^2=900=30^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A
\(\Delta DBC\) có:
DM là đường trung tuyến (M là trung điểm BC)
DM là đường trung trực (\(DM\perp BC\) tại M)
\(\Rightarrow\Delta DBC\) cân tại D
\(\Rightarrow\widehat{ABC}=\widehat{DCM}\)
Xét \(\Delta ABC\) và \(\Delta MCD\) có:
\(\widehat{BAC}=\widehat{CMD}=90^0\)
\(\widehat{ABC}=\widehat{DCM}\) (cmt)
\(\Rightarrow\Delta ABC\sim\Delta MCD\left(g-g\right)\)
b) Do M là trung điểm BC
\(\Rightarrow MC=\dfrac{BC}{2}=\dfrac{30}{2}=15\left(cm\right)\)
Do \(\Delta MCD\sim\Delta ABC\) (cmt)
\(\Rightarrow\dfrac{MC}{AB}=\dfrac{MD}{AC}=\dfrac{CD}{BC}\)
*) \(\dfrac{MC}{AB}=\dfrac{MD}{AC}\Rightarrow MD=\dfrac{MC.AC}{AB}=\dfrac{15.24}{18}=20\left(cm\right)\)
*) \(\dfrac{MC}{AB}=\dfrac{CD}{BC}\Rightarrow CD=\dfrac{MC.BC}{AB}=\dfrac{15.30}{18}=25\left(cm\right)\)