Bài 2:
a) Để hàm số đã cho làm hàm số bậc nhất thì 4 - 3m ≠ 0
⇔ -3m ≠ -4
⇔ m ≠ 4/3
b) Để hàm số đã cho làm hàm đồng biến thì 4 - 3m > 0
⇔ -3m > -4
⇔ m < 4/3
c) Để hàm số đã cho làm hàm nghịch biến thì 4 - 3m < 0
⇔ -3m < -4
⇔ m > 4/3
Bài 3
Thay tọa độ điểm A(1; 10) vào hàm số, ta có:
(4m² - 9).1 + 3 = 10
⇔ 4m² - 9 + 3 = 10
⇔ 4m² - 6 = 10
⇔ 4m² = 10 + 6
⇔ 4m² = 16
⇔ m² = 16 : 4
⇔ m² = 4
⇔ m = 2 hoặc m = -2
Thay tọa độ điểm A(-2; 3) vào hàm số, ta có:
(6m + 5).(-2) + m - 2 = 3
⇔ -12m - 10 + m - 2 = 3
⇔ -11m - 12 = 3
⇔ -11m = 3 + 12
⇔ -11m = 15
⇔ m = -15/11
Bài 5
a) Thay toạ độ điểm A(1; -2) vào hàm số, ta có:
a + b = -2
⇔ a = -2 - b (1)
Thay tọa độ điểm B(-1; 0) vào hàm số, ta có:
-a + b = 0 (2)
Thế (1) vào (2) ta được:
-(-2 - b) + b = 0
⇔ 2 + b + b = 0
⇔ 2 + 2b = 0
⇔ 2b = -2
⇔ b = -1
Thế b = -1 vào (1) ta được:
a = -2 - (-1) = -1
Vậy a = -1; b = -1
b) Do đồ thị hàm số cắt trục tung tại điểm có tung độ là 4 nên b = 4
y = ax + 4
Thay tọa độ điểm A(2; 1) vào hàm số ta được:
2a + 4 = 1
⇔ 2a = 1 - 4
⇔2a = -3
⇔ a = -3/2
Vậy a = -3/2; b = 4
c) Thay tọa độ điểm A(-1; -2) vào hàm số ta có:
-a + b = -2
⇔ b = -2 + a (1)
Thay tọa độ điểm B(3; 2) vào hàm số ta có:
3a + b = 2 (2)
Thế (1) vào (2) ta được:
3a + (-2 + a) = 2
⇔ 3a - 2 + a = 2
⇔ 4a - 2 = 2
⇔ 4a = 2 + 2
⇔ 4a = 4
⇔ a = 1
Thế a = 1 vào (1) ta được:
b = -2 + 1 = -1
Vậy a = 1; b = -1












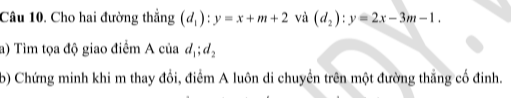 ai giup mik vs :<
ai giup mik vs :< 

 các bn giup mink với
các bn giup mink với
