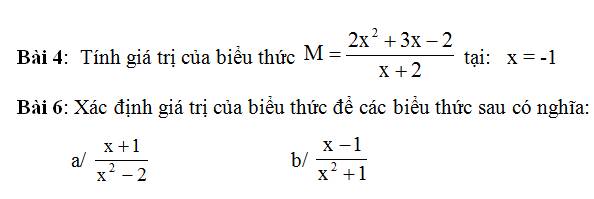Bài 4:
\(M=\dfrac{2x^2+3x-2}{x+2}\) (với \(x\ne-2\))
\(M=\dfrac{2x^2+4x-x-2}{x+2}\)
\(M=\dfrac{2x\left(x+2\right)-\left(x+2\right)}{x+2}\)
\(M=\dfrac{\left(x+2\right)\left(2x-1\right)}{x+2}\)
\(M=2x-1\)
Ta có: \(x=-1\left(tmdk\right)\)
Thay \(x=-1\) vào M ta có:
\(M=2\cdot-1-1=-2-1=-3\)
a) \(\dfrac{x+1}{x^2-2}\)
Có nghĩa khi \(x^2-2\ne0\)
\(\Rightarrow x^2\ne2\)
\(\Rightarrow\left[{}\begin{matrix}x\ne\sqrt{2}\\x\ne-\sqrt{2}\end{matrix}\right.\)
b) \(\dfrac{x-1}{x^2+1}\)
Có nghĩa khi:
\(x^2+1\ne0\)
Mà: \(x^2\ge0\) và \(1>0\)
\(\Rightarrow x^2+1\ge1\forall x\)
Nên biểu thức được xác định với mọi x