Đặt \(x-\dfrac{\pi}{4}=t\Rightarrow x=t+\dfrac{\pi}{4}\Rightarrow3x-\dfrac{\pi}{4}=3\left(t+\dfrac{\pi}{4}\right)-\dfrac{\pi}{4}=3t+\dfrac{\pi}{2}\)
\(\Rightarrow sin\left(3x-\dfrac{\pi}{4}\right)=sin\left(3t+\dfrac{\pi}{4}\right)=cos3t\)
Đồng thời: \(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=1-\dfrac{1}{2}sin^22x=1-\dfrac{1}{2}sin^2\left(2t+\dfrac{\pi}{2}\right)=1-\dfrac{1}{2}cos^22t\)
Nên pt trở thành:
\(1-\dfrac{1}{2}cos^22t+cost.cos3t-\dfrac{3}{2}=0\)
\(\Leftrightarrow-1-cos^22t+cos4t+cos2t=0\)
\(\Leftrightarrow-1-cos^22t+2cos^22t-1+cos2t=0\)
\(\Leftrightarrow cos^22t+cos2t-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2t=1\\cos2t=-2\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow2t=k2\pi\)
\(\Leftrightarrow t=k\pi\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
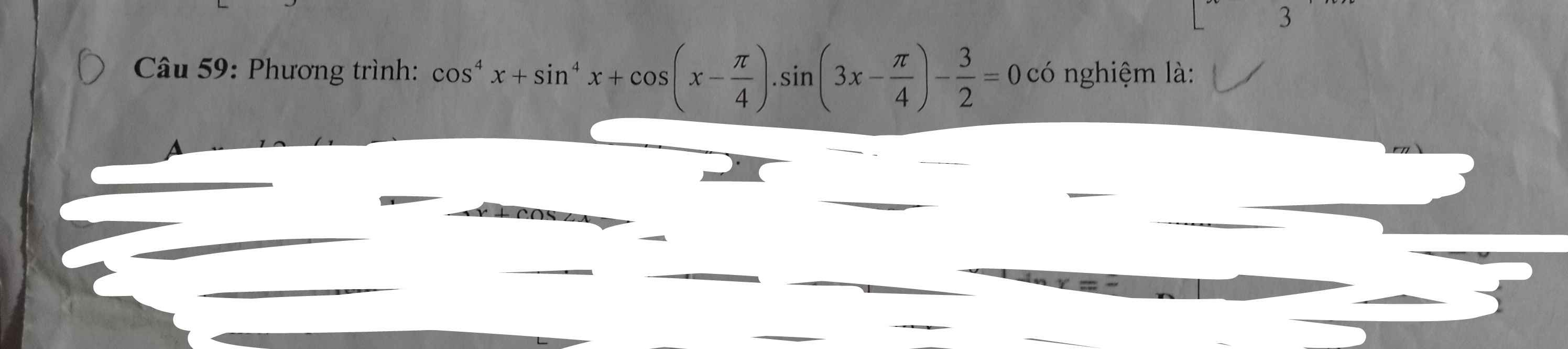
Ai giải chi tiết cái này hộ mình với