Bạn lưu ý chuyển bài toán vào đúng mục xác suất trong toán 11, không phải hàm số lượng giác.
Lời giải:
Gọi số có 3 chữ số phân biệt được lập từ $0,1,2,3$ là $\overline{a_1a_2a_3}$.
$A$ là tập hợp các số $\overline{a_1a_2a_3}$ mà $a_1$ có thể bằng $0,1,2,3$
$B$ là tập hợp các số $\overline{a_1a_2a_3}$ mà $a_1\neq 0$ (chính là số thỏa đề)
$C$ là tập các số $\overline{a_1a_2a_3}$ mà $a_1=0$
Tại tập $A$ thì mỗi số $0,1,2,3$ xuất hiện $18$ lần ở 3 vị trí hàng chục, trăm, đơn vị.
Tổng chữ số tập $A$:
$\frac{1}{3}.18(0+1+2+3)(10^2+10+1)=3996$
Tổng chữ số tập $C$ là:
$012+021+013+031+023+032=132$
Tồng các chữ số tập $B$ là:
$3996-132=3864$
Tổng các chữ số tập $B$:
$11988-132=11856$
Một hướng khác là bạn có thể viết ra $18$ số thỏa mãn đề và cộng lại với nhau.






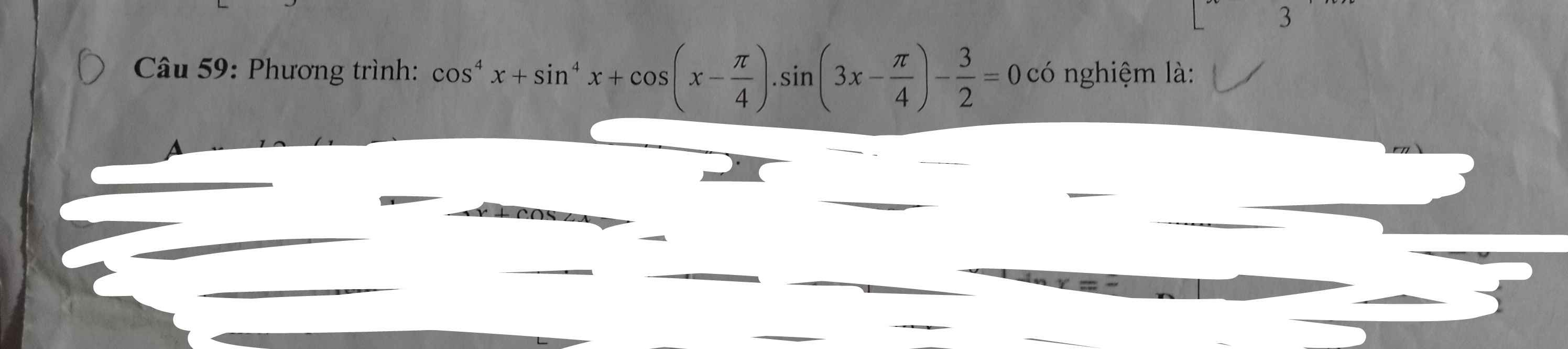



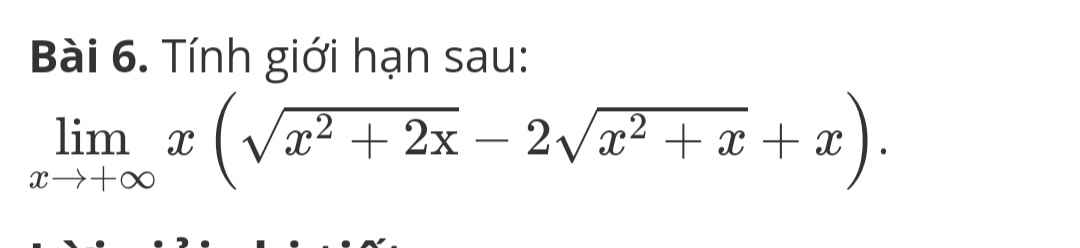


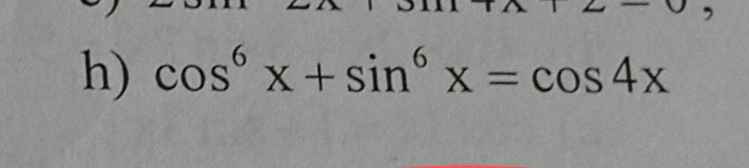 giai chi tiết giúp e với!!!
giai chi tiết giúp e với!!!