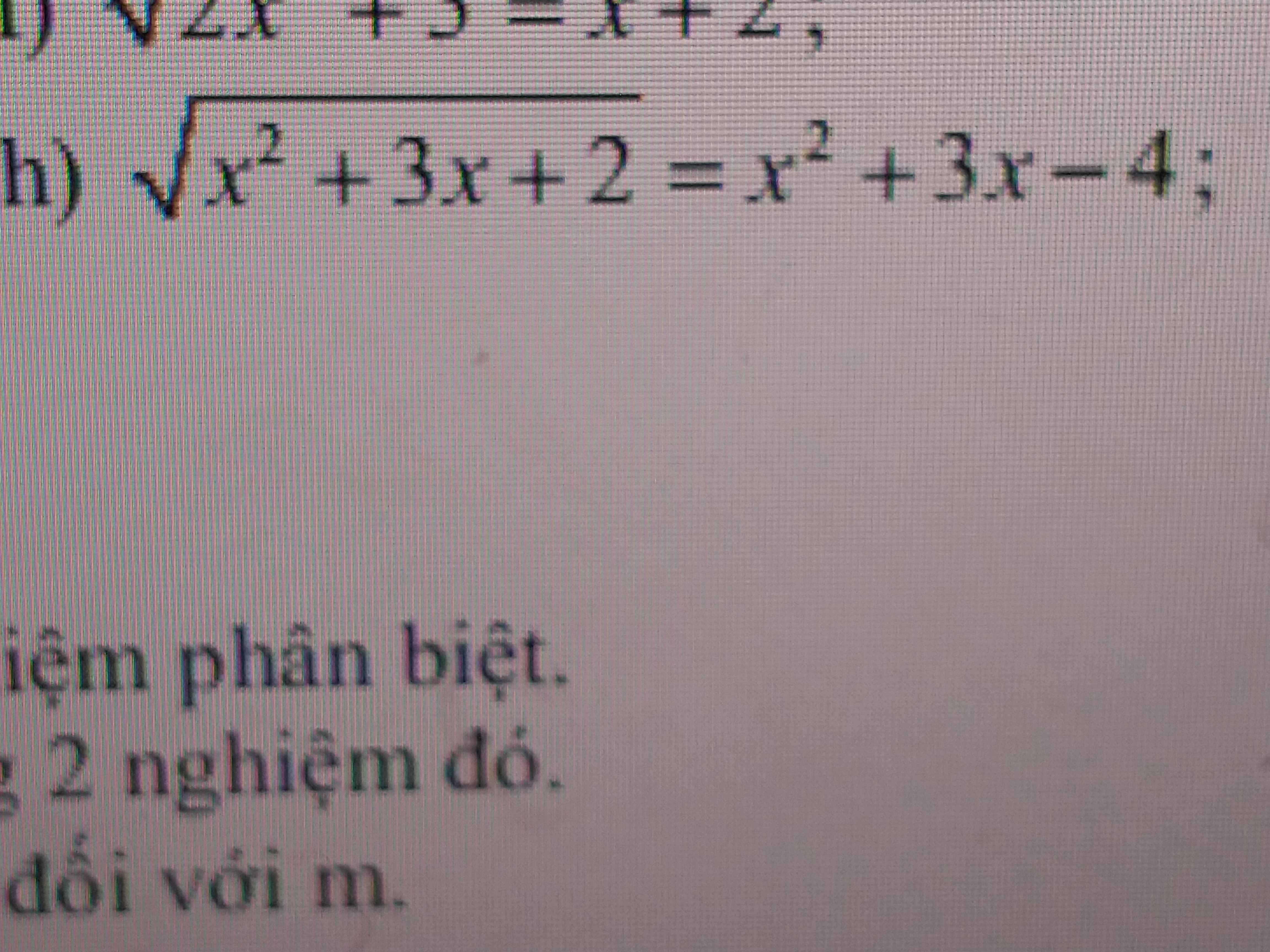ĐKXĐ: \(\left[{}\begin{matrix}x\ge-1\\x\le-2\end{matrix}\right.\)
Đặt \(\sqrt{x^2+3x+2}=t\ge0\Rightarrow x^2+3x=t^2-2\)
Pt trở thành:
\(t=t^2-2-4\)
\(\Leftrightarrow t^2-t-6=0\Rightarrow\left[{}\begin{matrix}t=3\\t=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2+3x+2}=3\)
\(\Leftrightarrow x^2+3x+2=9\)
\(\Leftrightarrow x^2+3x-7=0\) (bấm máy)
\(PT\Leftrightarrow\sqrt{x^2+3x+2}-3=x^2+3x-7\\ \Leftrightarrow\dfrac{x^2+3x-7}{\sqrt{x^2+3x+2}+3}-\left(x^2+3x-7\right)=0\\ \Leftrightarrow\left(x^2+3x-7\right)\left(\dfrac{1}{\sqrt{x^2+3x+2}+3}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+3x-7=0\\\sqrt{x^2+3x+2}+3=1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3\pm\sqrt{37}}{2}\\\sqrt{x^2+3x+2}=-2\left(\text{vô nghiệm}\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3+\sqrt{37}}{2}\\x=\dfrac{-3-\sqrt{37}}{2}\end{matrix}\right.\)
Thế vô PT ta thấy 2 nghiệm thỏa mãn
Vậy PT có nghiệm \(S=\left\{\dfrac{-3+\sqrt{37}}{2};\dfrac{-3-\sqrt{37}}{2}\right\}\)