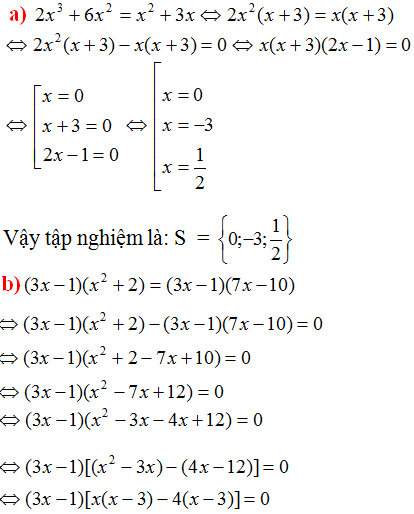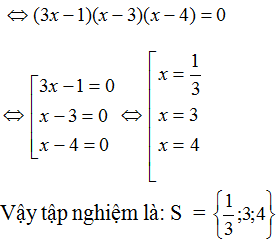a) \(2x^3 + 6x^2 = x^2 +3x\)
\(\Leftrightarrow2x^2\left(x+3\right)=x\left(x+3\right)\)
\(\Leftrightarrow2x^2\left(x+3\right)-x\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(2x^2-x\right)=0\)
\(\Leftrightarrow\left(x+3\right).x\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
S = \(\left\{-3;0;\dfrac{1}{2}\right\}\)
b) \((3x-1) (x^2 +2 ) = (3x-1) (7x - 10)\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2+2\right)-\left(3x-1\right)\left(7x-10\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2+2-7x+10\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2-7x+12\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\x-3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=3\\x=4\end{matrix}\right.\)
S = \(\left\{\dfrac{1}{3};3;4\right\}\)
a) 2x3+6x2 = x2 + 3x
<=> 2x2(x+3) = x(x+3)
<=> 2x2(x+3) - x(x+3)=0
<=>(x+3)(2x2-x)=0
<=>(3+x)x(2x-1)=0
<=> x=0 hay x+3=0 hay 2x-1=0
x=-3 x=1/2
x=1/2
S=(-3;1/2)
b)(3x-1)(x2+2) = (3x-1)(7x-10)
<=>(3x-1)(x2+2)-(3x-1)(7x-10)=0
<=> (3x-1)(x2-2-7x+10)=0
<=> (3x-1)(x2-7x+12)=0
<=> (3x-1)(x-3)(x-4)=0
<=> 3x-1= 0 hay x-3=0 hay x-4=0
<=> 3x=1 x=3 x=4
<=> x=1/3
S=(1/3;3;4)
a)2x3+6x2=x2+3x
⇔2x2(x+3)=x(x+3)
⇔2x2(x+3)-x(x+3)=0
⇔x(x+3)(2x-1)=0
⇔x=0 hoặc x+3=0 hoặc 2x-1=0
1.x=0
2.x+3=0⇔x=-3
3.2x-1=0⇔2x=1⇔x=0,5
vậy phương trình có 3 nghiệm:x=0 và x=-3 và x=0,5