Bài 6: Diện tích đa giác
Các câu hỏi tương tự
The volume of a cube is (8x^3+60x^2+150x+125)cm3. Find the total surface area of 3 such cube given that x>0
Tính diện tích tứ giác ABCD, biết góc C = 60 độ, CA là tia phân giác của góc C và CA = 4cm, CB = 3cm, CD = 5cm
Cho ∆MNP vuông tại N. Biết MN=6cm, NP=8cm, đường cao NH. Qua H kẻ HC vuông góc với MN, HD vuông góc với NP
a) Cmr: HDNC là hình chữ nhật
b) NH.MP=MN.NP
c) tính độ dài CD
d) tính diện tích ∆NMH
1, cho hình chữ nhật ABCD có AB=48,EC=ED, F thuộc AB. tính BF biết diện tích BFEC = 1/3 diện tích ABCD
2, cho hình thang ABCD có AB//CD, AB=4cm , CD = 9cm ,BD= 5cm, AC= 12cm
a, qua B kẻ // AC , cắt DC tại E . Tính góc DBE
b, Tính diện tích ABCD
Tính diện tích của hình được cho trong mỗi trường hợp sau đây :
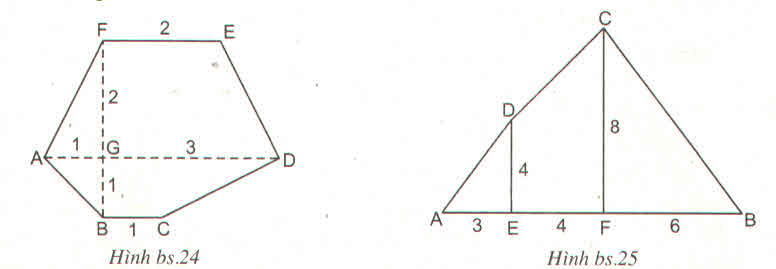
a) Đa giác ABCDEF, biết AD = 4cm, BC = 1cm, FE = 2cm, FB = 3cm, FB vuông góc với AD như hình bs.24
b) Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs.25)
Biết AB = 13 cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD
Cho tam giác ABC vuông góc với A(AB<AC);D,E lần lượt là trung điểm của BC và AC lấy F đối xứng với E qua D kẻ AH vuông góc với BC lấy M làm trung điểm của CH.
a) C/m:Tứ giác BECF là h.b.h
b) C/m:Tứ giác AEFB là h.c.n
c) C/m:AM vuông góc với MF
d) Tính S của các tứ giác BECF,AEFB,BF biết AB=6 cm,AC=8cm
( Đang cần gấp trong 4h45’chiều nay)
cho tam giác ABC vuông tại A có AB=30cm, AC=40cm. a) Tính Sabc. b) Gọi M,N trung điểm AB, AC. Tính Smncb
Giúp mình vs mn ơi.!
Cho tam giác ABC có BC = a, AC = b, AB = c, diện tích là S. Chứng minh rằng :
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)với \(p=\frac{a+b+c}{2}\)
cho hbh ABCD với diện tích và AB=a,BC=b.Lấy mỗi cạnh của hbh đó làm cạnh dựng 1 hình vuông ra phía ngoài hbh .Tính theo a,b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là canh của hbh đã cho.









