$Q=\Bigg(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\Bigg).\dfrac{\sqrt{x}+1}{\sqrt{x}}\,\,\,(x>0;\,x\ne 1;\, x\ne 2)\\=\Bigg[\dfrac{\sqrt{x}+2}{(\sqrt{x}+1)^2}-\dfrac{\sqrt{x}-2}{(\sqrt{x}-1)(\sqrt{x}+1)}\Bigg].\dfrac{\sqrt{x}+1}{\sqrt{x}}\\=\dfrac{(\sqrt{x}+2)(\sqrt{x}-1)-(\sqrt{x}-2)(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)^2}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\\=\dfrac{x+\sqrt{x}-2-(x-\sqrt{x}-2)}{(\sqrt{x}-1)(\sqrt{x}+1)}.\dfrac{1}{\sqrt{x}}\\=\dfrac{2\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}.\dfrac{1}{\sqrt{x}}\\=\dfrac{2}{x-1}$
Chương I - Căn bậc hai. Căn bậc ba
Các câu hỏi tương tự
Giúp em với ạ!
Em để đề bài ở dưới trả lời ạ.
Giúp em vs mn( giải câu cuối thôi ạ, đề dưới cmt)
Đề bài : trục căn thức ở mẫu
1) A= 3/3 căng 2 + 1
B= 1/3 căng 4 + 3 căng 2 + 1
mng giúp em với ạ , cảm ơn ạ
Đề bài: Tim x thuộc Z sao cho Q thuộc Z
ai làm dc câu nào cứ làm nhé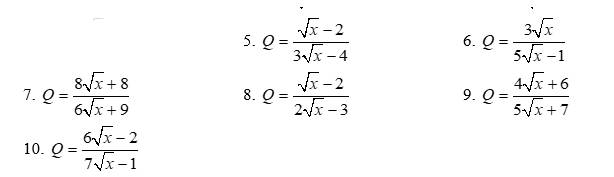
Tài liệu HSG Toán THCS anh gửi cho các em!
Hy vọng nó sẽ giúp các em ôn thi HSG tốt hơn!
https://drive.google.com/drive/folders/1gckARHUC5ZAqqGK4EPIOlP-dJYmOZKuK?usp=sharing

Mọi người giải giúp em với ạ, mai em thi rồi, mấy anh/chị giải thích rõ ràng giùm em nhé, em cảm ơn ạ.
Bài 1 : Cho Pdfrac{2-sqrt{x}}{3sqrt{x}}. Giả sử x là số nguyên. Tìm giá trị nhỏ nhất của P
Bài 2 : Cho ΔABC vuông tại A (AB AC). Đường tròn (O) đường kính AC cắt BC tại H
a) C/m : AH perp BC
b) Gọi M là trung điểm của AB. Chứng minh HM là tiếp tuyến của (O)
c) Tia phân giác của góc HAC cắt BC tại E và cắt (O) tại D. C/m : DA . DE DC2
d) Trường hợp AB 12 cm, AC 16 cm, tính bán kính đường tròn ngoại tiếp ΔAMH
Giúp em 2 câu c, d vớiii : Hình gửi ở dưới ạ
Đọc tiếp
Bài 1 : Cho \(P=\dfrac{2-\sqrt{x}}{3\sqrt{x}}\). Giả sử x là số nguyên. Tìm giá trị nhỏ nhất của P
Bài 2 : Cho ΔABC vuông tại A (AB < AC). Đường tròn (O) đường kính AC cắt BC tại H
a) C/m : AH \(\perp\) BC
b) Gọi M là trung điểm của AB. Chứng minh HM là tiếp tuyến của (O)
c) Tia phân giác của góc HAC cắt BC tại E và cắt (O) tại D. C/m : DA . DE = DC2
d) Trường hợp AB = 12 cm, AC = 16 cm, tính bán kính đường tròn ngoại tiếp ΔAMH
Giúp em 2 câu c, d vớiii :< Hình gửi ở dưới ạ
Giúp em với mn câu ỏi dưới phần bình luận
ai làm hộ tớ bài ở dưới với













