Question

CỨU 

Answer 1

Bài 7:

a: ta có; \(AK=KB=\frac{AB}{2}\)

\(DE=EC=\frac{DC}{2}\)

mà AB=CD(ABCD là hình bình hành)

nên AK=KB=DE=EC

Xét tứ giác AECK có

AK//CE

AK=CE

Do đó: AECK là hình bình hành

b: ABCD là hình bình hành

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

AECK là hình bình hành

=>AC cắt EK tại trung điểm của mỗi đường

mà O là trung điểm của AC

nên O là trung điểm của EK

=>E,O,K thẳng hàng

c: AECK là hình bình hành

=>AE//CK

=>EN//MC và KM//AN

Xét ΔBAN có

K là trung điểm của AB

KM//AN

Do đó: M là trung điểm của BN

=>BM=MN(1)

Xét ΔDMC có

E là trung điểm của DC

EN//MC

Do đó: N là trung điểm của DM

=>DN=NM(2)

Từ (1),(2) suy ra BM=MN=DN

d: Xét ΔACD có

DO,AE là các đường trung tuyến

DO cắt AE tại N

Do đó: N là trọng tâm của ΔACD

=>\(AN=\frac23AE\)

Xét ΔBAN có

K,M lần lượt là trung điểm của BA,BN

=>KM là đường trung bình của ΔABN

=>\(KM=\frac12AN=\frac12\cdot\frac23\cdot AE=\frac13AE\)

=>AE=3KM

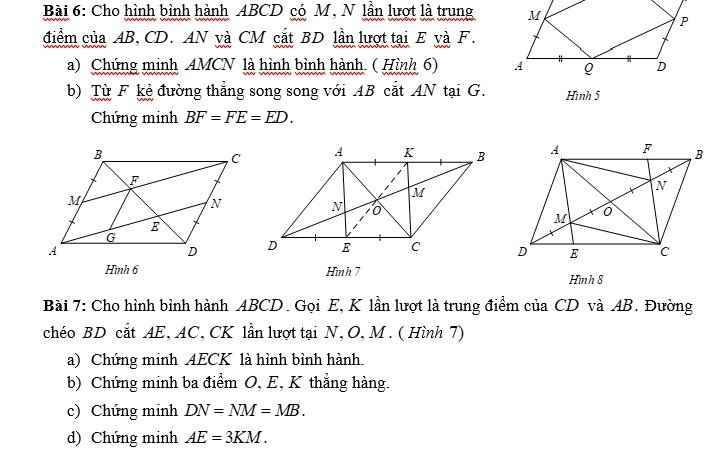
Bài 6:

a: ta có: \(AM=MB=\frac{AB}{2}\)

\(DN=NC=\frac{DC}{2}\)

mà AB=DC

nên AM=MB=DN=NC

Xét tứ giác AMCN có

AM//CN

AM=CN

Do đó: AMCN là hình bình hành

b: AMCN là hình bình hành

=>AN//MC

=>MF//AE và NE//FC

Xét ΔBAE có

M là trung điểm của BA

MF//AE

Do đó: F là trung điểm của BE

=>BF=FE(1)

Xét ΔDFC có

N là trung điểm của DC

NE//FC

Do đó: E là trung điểm của DF

=>DE=EF(2)

Từ (1),(2) suy ra BF=FE=ED