Có thể có phân số a/b (a, b ∈ Z, b ≠ 0) sao cho:
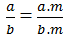
Vì 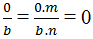
Có thể có phân số a/b (a, b ∈ Z, b ≠ 0) sao cho:
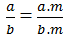
Vì 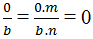
19. Cho phân số A= \(\dfrac{63}{3n+1}\)(n thuộc N)
a) Với giá trị nào của n thì A rút gọn được?
b) Với giá trị nào của n thì A là số tự nhiên.
tìm các số nguyên x, y thuộc vào Z biết:
\(\dfrac{x}{12}=\dfrac{3}{x}\)
1) Tìm số nguyên x, biết: \(\dfrac{x}{4}\)=\(\dfrac{16}{x}\) và x< 0.
2) Tìm các giá trị là số nguyên.
\(\dfrac{x-3}{x-1}\) có giá trị là số nguyên.
3) Cho A= \(\dfrac{n+8}{2n+5}\) (n ∈ N* ). Tìm các giá trị của n để A là số nguyên tố.
1) Cho A = 7+x / x-3
a, Tìm x thuộc Z để A là phân số
b, Tìm x thuộc Z để A là số nguyên
2) Tìm x,y thuộc Z :
a, x/5 = 2/y
b, x/7 = y/8 và y - x = 2
c, x/3 = y/4 và x + 2y = 22
Tìm x, y, z thuộc Z biết:
\(\dfrac{-4}{8}=\dfrac{x}{-10}=\dfrac{-7}{y}=\dfrac{z}{24}\)
Cho ba phân số \(\dfrac{1}{-2};\dfrac{5}{-3};\dfrac{3}{-4}\)
a) Viết ba phân số theo thứ tự các phân số trên và có mẫu là những số dương
b) Viết ba phân số theo thứ tự bằng các phân số trên và có mẫu là những số dương giống nhau
Cho biểu thức :
\(A=\dfrac{3}{n-2}\)
a) Tìm các số nguyên n để biểu thức A là phân số
b) Tìm các số nguyên n để A là một số nguyên
21. Tìm các số tự nhiên n để các phân số sau là phân số tối giản:
a)\(\dfrac{2n+3}{4n+1}\)
b)\(\dfrac{3n+2}{7n+1}\)
c) \(\dfrac{2n+7}{5n+2}\)
15. Tìm các số nguyên dương n nhỏ hơn 14 sao cho phân số n phần 14 có thể rút gọn được. Rút gọn phân số đó ứng với mỗi giá trị tìm được của n.
16. Viết các phân số tối giản a phần b (a>0, b>0), biết rằng ab = 36.
17.Tìm các phân số a phần b (a>0, b>0) có giá trị bằng: a) 21 phần 28, biết ƯCLN(a,b)=15 b) 21 phần 35, biết ƯCLN(a,b)=30. c) 36 phần 45, biết BCNN(a,b)=300. d) 15 phần 35, biết ƯCLN(a,b).BCNN(a,b)= 3549.