Ôn tập toán 8
Các câu hỏi tương tự
Cho P= 1^2017+2^2017+3^2017+...+2016^2017, Q= 1+2+3+4+...+2016. Chứng minh P chia hết cho Q
\(A=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2015}-\frac{1}{2016}+\frac{1}{2017}\)
\(B=\frac{1}{1009}+\frac{1}{1010}+...+\frac{1}{2016}+\frac{1}{2017}\)
Tính \(\left(A-B\right)^{2016^{2017}}\)
Cho \(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{2017^2}\)
\(B=\frac{2!}{3!}+\frac{2!}{4!}+\frac{2!}{5!}+...+\frac{2!}{2017!}\)
Chứng minh \(A+B< 2\)
a) Tính \(S=\left(-\frac{1}{7}\right)^0+\left(-\frac{1}{7}\right)^1+\left(-\frac{1}{7}\right)^2+...+\left(-\frac{1}{7}\right)^{2017}\)
b) So \(\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!}+...+\frac{99}{100!}\) với \(1\)
Tìm dư trong phép chia f(x)=x^2017+x^2016+1 cho
a) x−1 b) x^2−1
M=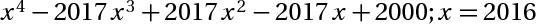
N=3/229*(2+1/433) - 1/229 * 432/433 -4/299*433giúp tớ với
Xem chi tiết
Rút gọn B = \(\left[\frac{0,4-\frac{2}{9}+\frac{2}{11}}{1,4-\frac{7}{9}+\frac{7}{11}}-\frac{\frac{1}{3}-0,25+\frac{1}{5}}{1\frac{1}{6}-0,875+0,7}\right]:\frac{2016}{2017}\)
Tìm x biết: |x-2016| -|x-2017| =1
Tìm dư trong phép chia \(f\left(x\right)=x^{2017}+x^{2016}+1\) cho
a) \(x-1\)
b) \(x^2-1\)