Question

C/m nếu AB+CD=AD+BC thì tứ giác ABCD ngoại tiêps đường tròn.

Answer 1

Answer 2

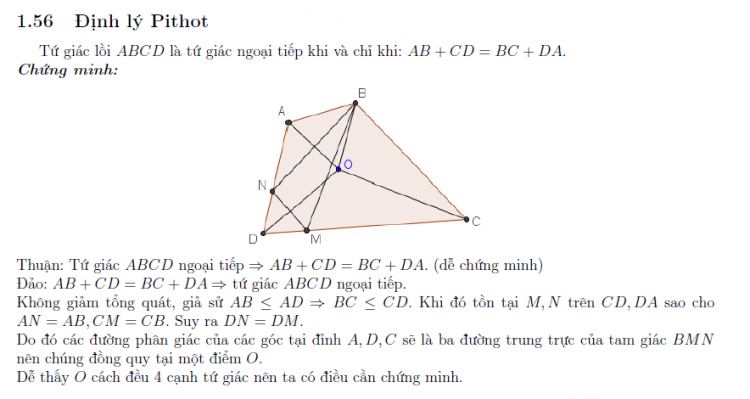
Dễ dàng thấy rằng nếu ABCD ngoại tiếp được một đường tròn thì $AB + CD = AD + BC$ điều này có được theo tính chất tiếp tuyến

Giả sử ABCD thoả mãn điều kiện $AB + CD = AD + BC$ .

Suy ra $|AD - CD| = |AB - BC| = 2a$ $(a \in R^+)$ . Bằng cách vẽ hai đường phân giác các góc A và B , ta dựng được đường tròn tiếp xúc với AB , AD và BC. Gọi D là điểm trên AD sao cho ABCD ngoại tiếp đường tròn này .

Ta có $AB + CD' = AD' + BC$ , suy ra $|AD' – CD' =|AB - BC| = 2a$. Như vậy , cả D và D đều nằm trên Hyperbol có hai tiêu điểm A và C . Tuy nhiên, vì A , D , D thẳng hàng nên D' phải trùng D , suy ra điều phải chứng minh .