Xét ΔDKE và ΔDHF có
DK=DH
\(\widehat{K}=\widehat{H}\)
KE=FH
Do đó: ΔDKE=ΔDHF
Xét ΔDKE và ΔDHF có
DK=DH
\(\widehat{K}=\widehat{H}\)
KE=FH
Do đó: ΔDKE=ΔDHF
Hình tam giác ABC. Tia phân giác góc A cắt BC tại D, vẽ DE//AB, DF//AC (E thuộc AC, F thuộc AB) chứng minh DA là tia phân giác EDF
Cho tam giác ABC. Qua đỉnh A vẽ đường thẳng a song song với BC. Qua đỉnh B vẽ đường thẳng b song song với AC. Hỏi vẽ được mấy đường thẳng a, mấy đường thẳng b, vì sao ?![]()
Cho tam giác ABC, điểm M trên cạnh BC. Vẽ tia ME // AB (E thuộc AC), MF // AC
(F thuộc AB). Xác định vị trí của điểm M để trên tia MA là tia phân giác của góc
EMF ?
Cho tam giác ABC. Qua đỉnh A vẽ đường thẳng a song song với BC, qua đỉnh B vẽ đường thẳng b song song với AC. Hỏi vẽ được mấy đường thẳng a, mấy đường thẳng b ? Vì sao ?
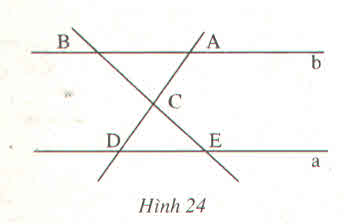
Cho hình 24 (a //b). Hãy nêu tên các cặp góc bằng nhau của hai tam giác CAB và CDE ?
Cho tam giác DEF vuông tại D, có DE=DF. Gọi H là trung điểm của cạnh EF a,CM tam giác DHE=tam giác DHF và DH vuông góc với EF b, Từ F kẻ đường vuông góc với EF, nó cắt tia ED tại G. CM GF//DH. c,CM FG=FE giúp nhanh vs
Cho tam giác ABC , D ∈ BC . Kẻ DE // AB ( E ∈ BC ). Kẻ DF // BC ( F ∈ AB )
a) Tìm các góc đỉnh D bằng các góc của tam giác ABC .
b) Tính tổng 3 góc của tam giác ABC .
Cho tam giác ABC, kẻ trung tuyến BD, CE. Trên tia đối của tia DB lấy điểm M sao cho DM = DB. Trên tia đối của tia EC lấy điểm N sao cho EN = EC.
Chứng minh:
a) Tam giác ADM = Tam giác CDB, AM song song vs BC.
b) Ba điểm N, A, M thẳng hàng.
c) A trung điểm MN.
Cho tam giác ABC
Chứng minh: A+B+C=180 độ