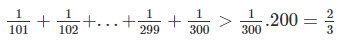Bài 11: Tính chất cơ bản của phép nhân phân số
Các câu hỏi tương tự
chứng tỏ rằng 1/101+1/102+........+1/299+1/300>2/3
Chứng tỏ rằng :
\(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+....+\dfrac{1}{17}< 2\)
chứng tỏ rằng 1/ 101+ 1/102+ 1/103+ 1/104+... + 1/299+ 1/300> 2/3
đừng chép mạng
\(A=\dfrac{1}{2}x\dfrac{1}{7}+\dfrac{1}{7}x\dfrac{1}{12}+\dfrac{1}{12}x\dfrac{1}{17}+....+\dfrac{1}{2002}x\dfrac{1}{20007}\\ B=(1+\dfrac{1}{2})x(1+\dfrac{1}{3})...(1+\dfrac{1}{2007})\\ C=(1-\dfrac{1}{2})x(1-\dfrac{1}{3})...(1-\dfrac{1}{2008})\)
Trong các đẳng thức sau đây, đẳng thức minh họa tính chất kết hợp của phép nhân phân số đó là :
(A) dfrac{1}{3}.dfrac{1}{5}.dfrac{1}{2}dfrac{1}{3}.dfrac{1}{2}.dfrac{1}{5} (B) left(dfrac{1}{3}.dfrac{1}{5}right).dfrac{1}{2}dfrac{1}{3}.left(dfrac{1}{5}.dfrac{1}{2}right)
(C) dfrac{1}{3}.dfrac{1}{5}+dfrac{1}{3}.dfrac{1}{2}dfrac{1}{3}.left(dfrac{1}{5}+dfrac{1}{2}right) (D) dfrac{1}{3}.dfrac{1}{5}.dfrac{1}{2}left(dfrac{1}{3}.dfrac{1}{5}right).left(dfr...
Đọc tiếp
Trong các đẳng thức sau đây, đẳng thức minh họa tính chất kết hợp của phép nhân phân số đó là :
(A) \(\dfrac{1}{3}.\dfrac{1}{5}.\dfrac{1}{2}=\dfrac{1}{3}.\dfrac{1}{2}.\dfrac{1}{5}\) (B) \(\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\dfrac{1}{2}=\dfrac{1}{3}.\left(\dfrac{1}{5}.\dfrac{1}{2}\right)\)
(C) \(\dfrac{1}{3}.\dfrac{1}{5}+\dfrac{1}{3}.\dfrac{1}{2}=\dfrac{1}{3}.\left(\dfrac{1}{5}+\dfrac{1}{2}\right)\) (D) \(\dfrac{1}{3}.\dfrac{1}{5}.\dfrac{1}{2}=\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\left(\dfrac{1}{3}.\dfrac{1}{2}\right)\)
Hãy chọn đáp án đúng ?
Áp dụng các tính chất của phép nhân phân số để tính nhanh :
\(M=\dfrac{8}{3}.\dfrac{2}{5}.\dfrac{3}{8}.10.\dfrac{19}{92}\)
\(N=\dfrac{5}{7}.\dfrac{5}{11}+\dfrac{5}{7}.\dfrac{2}{11}-\dfrac{5}{7}.\dfrac{14}{11}\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right).\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
\(1+\dfrac{1}{2}.\dfrac{3.2}{2}+\dfrac{1}{3}.\dfrac{4.3}{2}+...+\dfrac{1}{500}.\dfrac{501.500}{2}\)
Các bn giải hộ mk vs ạ. Mai mik pk nộp rùi
CẢM ƠN CÁC BN RẤT NH!!!
Tính giá trị các biểu thức sau một cách hợp lí :
\(A=\dfrac{7}{19}.\dfrac{8}{11}+\dfrac{7}{19}.\dfrac{3}{11}+\dfrac{12}{19}\)
\(B=\dfrac{5}{9}.\dfrac{7}{13}+\dfrac{5}{9}.\dfrac{9}{13}-\dfrac{5}{9}.\dfrac{3}{13}\)
\(C=\left(\dfrac{67}{111}+\dfrac{2}{33}-\dfrac{15}{117}\right).\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)
Tính giá trị các biểu thức sau :
\(A=a.\dfrac{1}{2}+a.\dfrac{1}{3}-a.\dfrac{1}{4}\) với \(a=\dfrac{-4}{5}\)
\(B=\dfrac{3}{4}.b+\dfrac{4}{3}.b-\dfrac{1}{2}.b\) với \(b=\dfrac{6}{19}\)
\(C=c.\dfrac{3}{4}+c.\dfrac{5}{6}-c.\dfrac{19}{12}\) với \(c=\dfrac{2002}{2003}\)