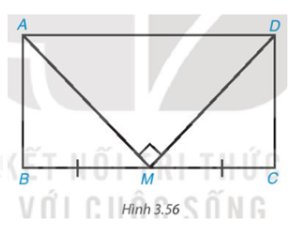
Xét các tam giác AEH, BEF, CGF, DGH có:
\( \widehat A = \widehat B = \widehat C = \widehat D = 90^0\)
AE = BE = CG = DG (vì E, G là trung điểm của AB, CD và AB = CD)
BF = FC = DH = HA (vì F, H là trung điểm của BC, AD và BC = AD)
\( \Rightarrow \Delta AEH = \Delta BEF = \Delta CGF = \Delta DGH \)
Suy ra EH = EF = FG = GH (các cạnh tương ứng) nên tứ giác EFGH là hình thoi (vì có 4 cạnh bằng nhau).