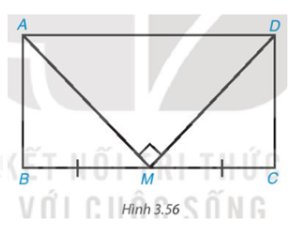
Do ABCD là hình chữ nhật nên \(\left\{{}\begin{matrix}AB=CD\\AD=BC\end{matrix}\right.\)
Mà M là trung điểm BC ⇒ \(\left\{{}\begin{matrix}MA=MD\\MB=MC\end{matrix}\right.\) (1)
Áp dụng định lí Py-ta-go trong tam giác ABM, MCD, AMD, ta có:
\(\left\{{}\begin{matrix}AB^2+MB^2=AM^2\\CD^2+MC^2=MD^2\\AM^2+MD^2=AD^2\end{matrix}\right.\) (2)
Từ (1) và (2), ta có:
\(2AB^2+2BM^2=AD^2=BC^2=4BM^2\)
\(\Rightarrow AB=BM=\dfrac{1}{2}BC\)
Mà \(2\cdot\left(AB+BC\right)=36\)
⇒ AB = 6 (cm) và BC = 12 (cm).