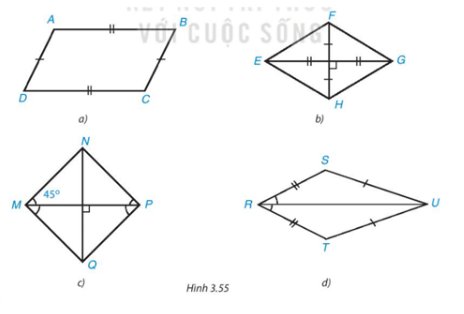
• Hình 3.51a)
Tứ giác đã cho có hai đường chéo cắt nhau tại trung điểm của mỗi đường và chúng vuông góc với nhau nên tứ giác đó là hình thoi.
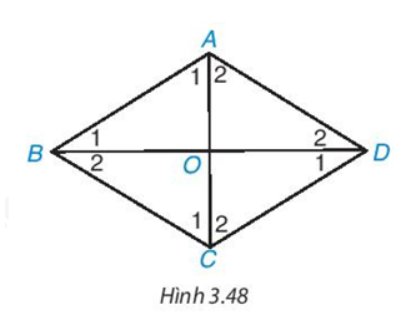
• Gọi tứ giác trong Hình 3.51b) là tứ giác ABCD.
Vì \(\widehat {{B_1}} = \widehat {{D_1}}\) mà hai góc này ở vị trí so le trong nên AB // CD.
Mà AB = CD nên tứ giác ABCD là hình bình hành.
Mặt khác, \(\widehat {{D_1}} = \widehat {{D_2}}\) hay DB là tia phân giác của \(\widehat {A{\rm{D}}C}\)
Khi đó, hình bình hành ABCD có DB là tia phân giác của \(\widehat {A{\rm{D}}C}\).
Do đó tứ giác ABCD là hình thoi.
• Tứ giác trong Hình 3.51c) hai đường chéo vuông góc với nhau và có đường chéo là đường vuông góc của một góc của tứ giác.
Từ đó ta suy ra tứ giác đã cho không phải là hình thoi.
Vậy Hình 3.51a và Hình 3.51b là hình thoi.