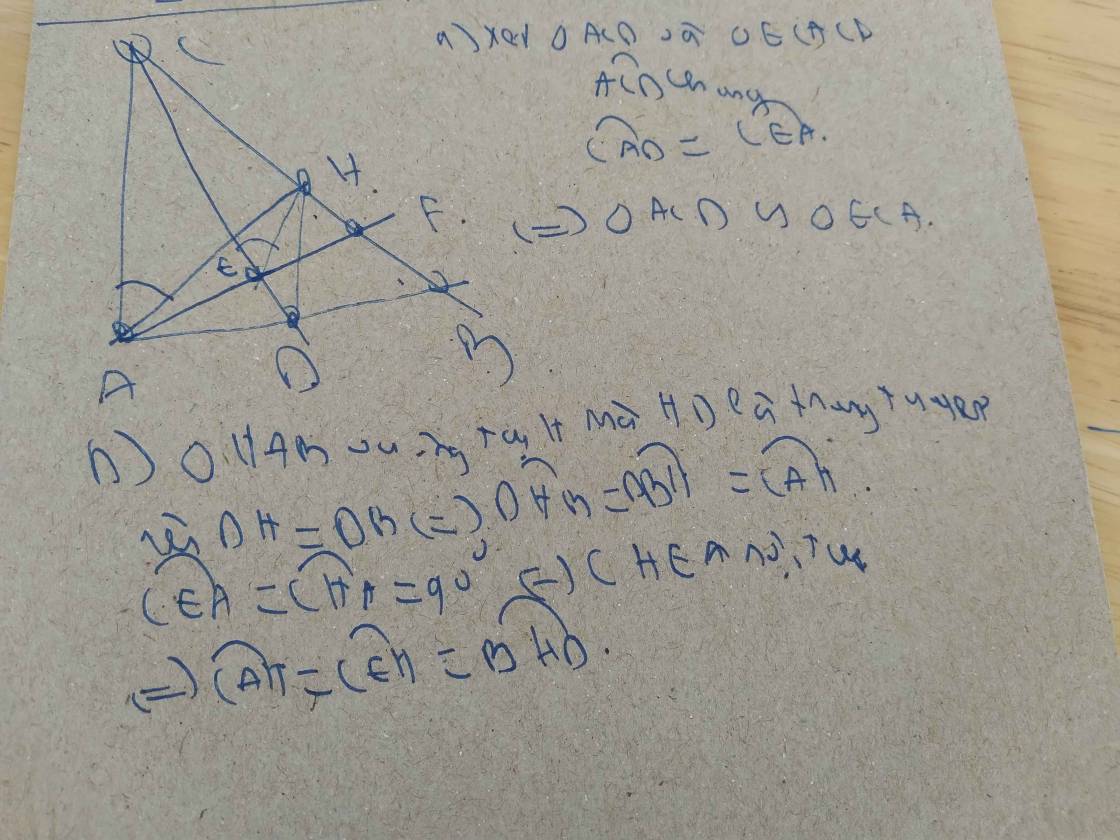Ôn tập: Tam giác đồng dạng
Các câu hỏi tương tự
cho tam giác ABC vuông tại A (AB<AC) có đường cao AH (H thuộc BC). Lấy điểm D sao cho H là trung điểm của đoạn thẳng BD. Chứng minh tam giác ABC đồng dạng với tam giác HBA. Qua điểm C kẻ đường thẳng vuông góc với tia AD tại E. Chứng minh AH.CD=CE.AD. Chứng minh tam giác HDE đồng dạng tam giác ADC và BD.AC=2AD.HE. Tia AH cắt tia CE tại F chứng minh AF^2=2BF.AE
Cho tam giác ABC vuông tại A, có AB= 8cm, đường cao AH. Tia phân giác của góc C cắt AB tại D.
a) Chứng minh tam giác HBA đồng dạng với tam giác ABC
b) Tính BC, BD, AD
c) Từ B vẽ BK vuông góc với CD tại K, BK cắt AH kéo dài tại E, trên CD lấy điểm S sao cho BA=BS. Chứng minh BF vuông góc với EF
Cho tam giác ABC vuông tại A (AB>AC). Kẻ đường cao AH (H thuộc BC). Gọi D là trung điểm của AB. Qua A kẻ đường thẳng vuông góc với CD cắt CD và CB lần lượt tại E và F. Gọi K là hình chiếu vuông góc của D trên BC.
1) Chứng minh rằng các tam giác ADE và CDA đồng dạng với nhau.
2) Chứng minh rằng BD.BC = BE.CD.
Cho tam giác ABC vuông tại A ( AB<AC) đường cao AH
a/ Chứng minh tam giác BHA đồng dạng tam giác BAC
b/ Vẽ BD là đường phân giác của góc tam giác ABC cắt AH tại K. Chứng minh : BA.BK = BD.BH
c/ Qua C kẻ đường thẳng vuông góc với BD tại E. Chứng minh AE = EC
cho tam giác ABC vuông tại A ( AB<AC) có đường cao AH. Gọi M là trung điểm của AC, BM cắt AH tại I. vẽ AK vuông góc với BM tại K,
a) chứng minh : tam giác BHI đồng dạng với tam giác AKI và IB. IK = IA.IH
b) chứng minh: góc BAH = góc BKH
c) tia AK cắt BC tại D. Chứng minh: HD.KC = HK.DC
Cho tam giác ABC vuông tại A , đường cao AH .Đường phân giác củ góc ABC cắt AC tại D và cắt AH tại E A) Chứng minh tam giác ABC đồng dạng tam giácHBA và AB^2=BC.BH B) biết AB =9cm, BC= 15cm. Tính DC và AD C) gọi I là trung điểm của ED .Chứng minh : BIH=ACB Hộ mk với ạ 😢 Vẽ hình hộ mik luôn mai mik thi òi ạ Thank m.n
Cho tam giác ABC vuông tại A và có đường cao AH.
a/ Chứng minh AHC đồng dạng với BAC và suy ra AH.BC=AB. AC
b/ Gọi CD là đường phân giác của góc ACB (D thuộc cạnh AB). CD cắt AH tại E. Chứng minh rằng: tam giác ACE đồng dạng với tam giác BCD.
c/ Gọi I là trung điểm của đoạn thẳng DE. Chứng minh rằng: AI vuông góc DE
Cho tam giác ABC vuông tại A ( AC > AB ), đường cao AH. Trên tia HC lấy điểm D sao cho HD = AH. Qua D kẻ đường thẳng vuông góc với BC, cắt cạnh AC tại E.
a) Chứng minh tam giác ABC đồng dạng với tam giác HAC
b) Chứng minh EC . AC = DC. BC
c) Chứng minh tam giác BEC = tam giác ADC và tam giác ABE vuông cân
Bài 4: Cho tam giác ABC vuông tại A đường cao AH . a) Chứng minh tam giác AHB đồng dạng tam giác ABC b) Gọi M , N lần lượt là trung điểm của BC và AB . Đường vuông góc BC kẻ từ B cắt MN tại I . Chứng minh c) IC cắt AH tại O . Chứng minh O là trung điểm AH d) Gọi K là giao điểm của CA và BI . Tính độ dài BK ,biết AB 15 cm , AC 20 cm .
Đọc tiếp
Bài 4: Cho tam giác ABC vuông tại A đường cao AH .
a) Chứng minh tam giác AHB đồng dạng tam giác ABC
b) Gọi M , N lần lượt là trung điểm của BC và AB . Đường vuông góc BC kẻ từ B cắt MN tại I . Chứng minh
c) IC cắt AH tại O . Chứng minh O là trung điểm AH
d) Gọi K là giao điểm của CA và BI . Tính độ dài BK ,biết AB = 15 cm , AC = 20 cm .