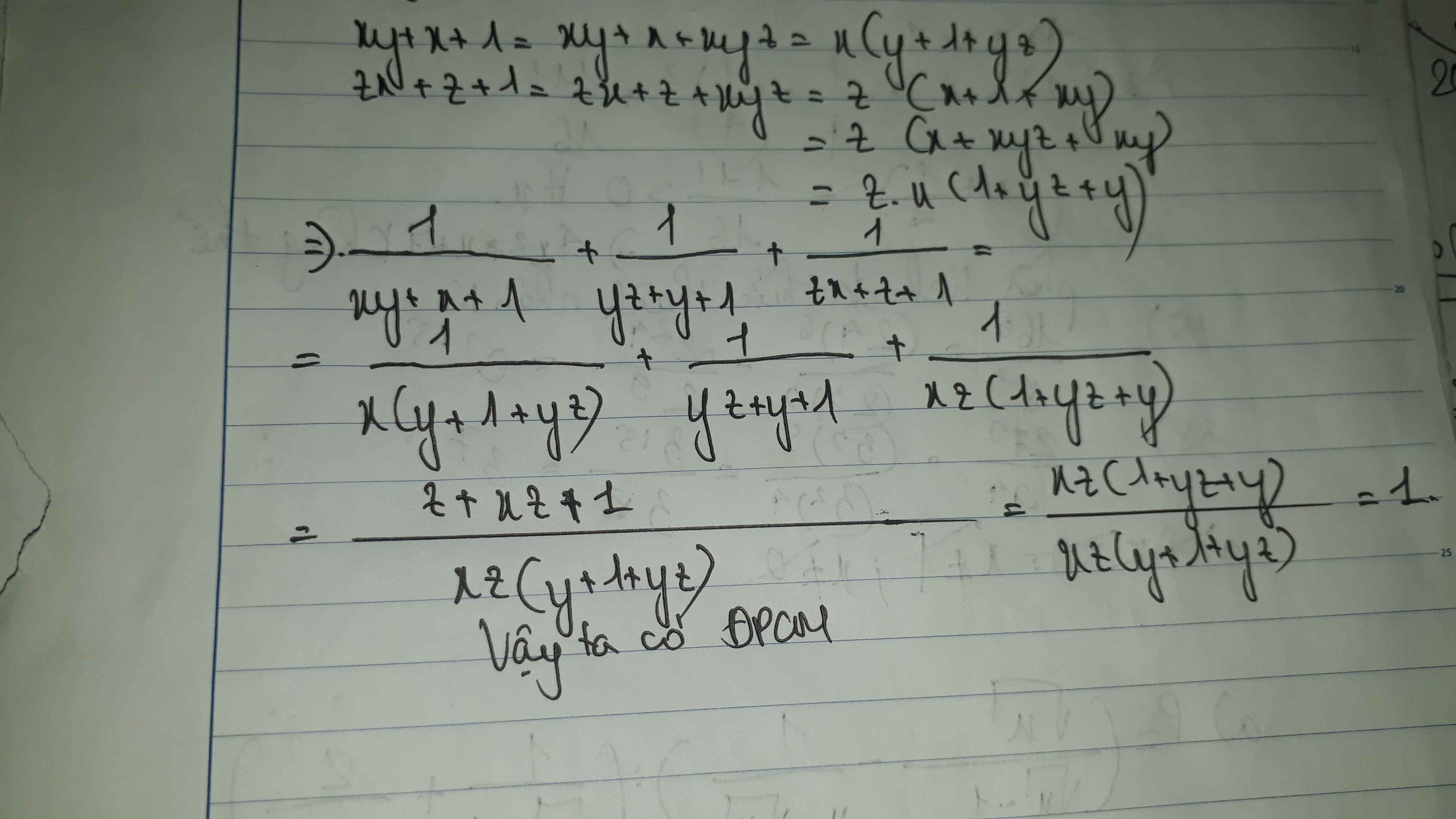17 tháng 7 2021 lúc 15:00
Ôn thi vào 10
Các câu hỏi tương tự
Cho các số thực dương x, y, z thỏa mãn x3 + y3 + z3 = 24. Tìm GTNN của biểu thức
\(M=\dfrac{xyz+2\left(x+y+z\right)^2}{xy+yz+zx}-\dfrac{8}{xy+yz+zx+1}\)
cho các số thực dương thoả mãn: \(\sqrt{x}+\sqrt{y}+\sqrt{z}=1\)
CMR: \(\sqrt{\dfrac{xy}{x+y+2z}}+\sqrt{\dfrac{yz}{y+z+2x}}\sqrt{\dfrac{zx}{z+x+zy}}\le\dfrac{1}{2}\)
Cho các số thực dương x, y, z thỏa mãn x+y+z=4 . Chứng minh rằng: \(\dfrac{1}{xy}+\dfrac{1}{xz}\ge1\)
Cho x,y,z là các số thực dương thỏa mãn x + y +z ≥ 2019 . Tìm giá trị nhỏ nhất của biểu thức T = \(\dfrac{x^2}{x+\sqrt{yz}}\) + \(\dfrac{y^2}{y+\sqrt{zx}}\) + \(\dfrac{z^2}{z+\sqrt{xy}}\)
Cho các số thực x, y,z thỏa mãn 0 ≤ x,y,z ≤ 1 . Chứng minh rằng
x + y + z - 2( xy + yz + zx ) + 4xyz ≤ 1
Cho x,y,z dương thỏa mãn \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=3\) . Chứng minh rằng \(\dfrac{1}{\sqrt{2x^2+y^2+3}}+\dfrac{1}{\sqrt{2y^2+z^2+3}}+\dfrac{1}{\sqrt{2z^2+x^2+3}}\) ≤ \(\dfrac{\sqrt{6}}{2}\)
cho các số dương X,Y,Z thỏa mãn :x\(^3\)+Y\(^3\)+Z\(^3\)=1
chứng minh rằng; \(\dfrac{X^2}{\sqrt{1-X^2}}\)+\(\dfrac{Y^2}{\sqrt{1-Y^2}}\)+\(\dfrac{Z^2}{\sqrt{1-Z^2}}\)\(\ge\)2
cho x,y,z là các số thực dương thỏa mãn \(x^2+y^2+z^2\ge\dfrac{1}{3}\)
chứng minh \(\dfrac{x^3}{2x+3y+5z}+\dfrac{y^3}{2y+3z+5x}+\dfrac{z^3}{2z+3x+5y}\ge\dfrac{1}{30}\)
cho x,y>0 thỏa mãn: x+y=1
tìm Min \(A=\dfrac{1}{x^2+y^2}+\dfrac{1}{xy}\)