a:Ta có: BA=BC
DC=DA
Do đó: BD là đường trung trực của AC
b: Xét ΔABD và ΔCBD có
AB=CB
BD chung
AD=CD
Do đo: ΔABD=ΔCBD
Suy ra: \(\widehat{BAD}=\widehat{BCD}=\dfrac{360^0-100^0-70^0}{2}=95^0\)
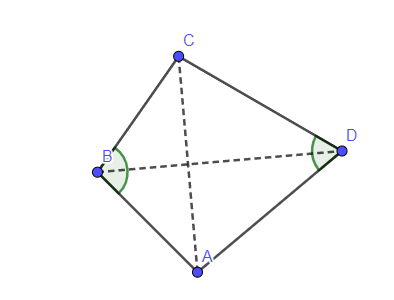
`a)` Ta có :
`BA=BC` \((gt)\)
`=>B in` đg trung trực `AC`
`DA=DC`\((gt)\)
`=>D in` đg trung trực `AC`
`=>BD` là đg trung trực `AC`
`b)` Xét \(\Delta BAD\) và \(\Delta BCD\) có :
`BA=BC`\((gt)\)
`DA=DC`\((gt)\)
`BD` chung
Do đó : \(\Delta BAD=\Delta BCD\left(c.c.c\right)\\ \Rightarrow\widehat{BAD}=\widehat{BCD}\)
\(\widehat{BAD}+\widehat{BCD}+\widehat{ABC}+\widehat{ADC}=360^0\\ \widehat{BAD}+\widehat{BCD}=360^0-\left(\widehat{ABC}+\widehat{ADC}\right)\\ 2\widehat{BAD}=360^0-\left(100^0+70^0\right)\\ 2\widehat{BAD}=190^0\\ \widehat{BAD}=\dfrac{190^0}{2}=95^0\\ \widehat{BAD}=\widehat{BCD}=95^0\)
hình vẽ sơ để dễ hình dung thôi với lại góc ko ghi mũ được
a/ ta có
AB=BC →B thuộc đường trung trực của AC(tính chất điểm nằmg trên đường trung trực của 1 đoạn thẳng)
CD=DA →D thuộc đường trung trực của AC(tính chất điểm nằmg trên đường trung trực của 1 đoạn thẳng)
suy ra BD là đường trung trực của đoạn thẳng AC
b/ tứ giác ABCD có
A + B+C + D=360 độ
→A+C=360-(B+D)
A + C = 360-(100+70)
A + C = 360-170
vậy A + C = 190 độ
xét ΔBAD và ΔBAC có
AB=BC
CD=DA
BD chung
→ΔBAD = ΔBAC(c.c.c)
→ góc A= góc C
mà A+C=190
→A=C=190/2=95
Vậy A=C=95 độ


















