Question

Cho tứ giác \(ABCD\) có các cạnh đối song song. Gọi \(O\) là giao điểm của hai đường chéo. Hãy chứng tỏ:

- Tam giác \(ABC\) bằng tam giác \(CDA\)

- Tam giác \(OAB\) bằng tam giác \(OCD\)

Answer 1

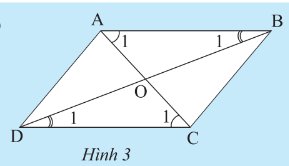
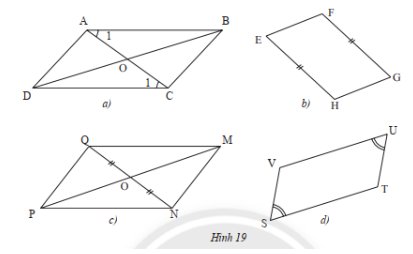
Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:

\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))

\(AC\) chung

\(\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}\) (do \(AD\) // \(BC\))

Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c)

Xét \(\Delta OAB\) và \(\Delta OCD\) ta có:

\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))

\(AC\) chung

\(\widehat {{{\rm{B}}_{\rm{1}}}} = \widehat {{{\rm{D}}_{\rm{1}}}}\) (do \(\Delta ABC = \Delta CDA\))

Suy ra: \(\Delta OAB = \Delta OCD\) (g-c-g)