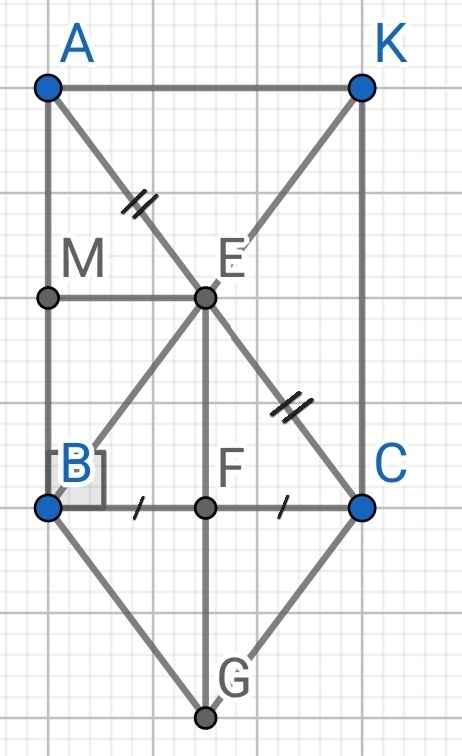
Cho tam giác ABC vuông tại B .Gọi E,F lần lượt là trung điểm của AC,BC.Kẻ Ex song song với BC cắt AB tại M
a)Chứng minh BMEF là hình chữ nhật
b)Gọi K đối xứng với B qua E .Tứ giác BAKC là hình gì?Vì sao?
c)Gọi G đối xứng với E qua F .Tứ giác BGCE là hình gì ?Vì sao?
d)Tam giác ABC cần thêm điều kiện gì để tứ giác BGCE là hình vuông?
a) ∆ABC vuông tại B (gt)
⇒ AB ⊥ BC
⇒ BM ⊥ BF
⇒ ∠MBF = 90⁰
Do EM // BC (gt)
⇒ EM // BF
EM // BC (gt)
E là trung điểm của AC (gt)
⇒ M là trung điểm của AB
⇒ EM là đường trung bình của ∆ABC
⇒ EM = BC : 2
F là trung điểm của BC (gt)
⇒ BF = CF = BC : 2
⇒ EM = BF = BC : 2
Tứ giác BMEF có:
EM // BF (cmt)
EM = BF = BC : 2 (cmt)
⇒ BMEF là hình bình hành
Mà ∠MBF = 90⁰ (cmt)
⇒ BMEF là hình chữ nhật
b) Do K đối xứng với B qua E (gt)
⇒ E là trung điểm của BK
Tứ giác BAKC có:
E là trung điểm của BK (cmt)
E là trung điểm của AC (gt)
⇒ BAKC là hình bình hành
Mà ∠ABC = 90⁰ (gt)
⇒ BAKC là hình chữ nhật
c) Do G đối xứng với E qua F (gt)
⇒ F là trung điểm của EG
∆ABC vuông tại B (gt)
E là trung điểm của AC (gt)
⇒ BE là đường trung tuyến ứng với cạnh huyền AC
⇒ BE = CE = AC : 2
Tứ giác BGCE có:
F là trung điểm của BC (gt)
F là trung điểm của EG (cmt)
⇒ BGCE là hình bình hành
Mà BE = CE (cmt)
⇒ BGCE là hình thoi
d) Để BGCE là hình vuông thì BE ⊥ CE
⇒ BE là đường cao của ∆ABC
Mà BE là đường trung tuyến của ∆ABC (cmt)
⇒ ∆ABC cân tại B
Lại có ∆ABC vuông tại B (gt)
⇒ ∆ABC vuông cân tại B
\(a,\left\{{}\begin{matrix}BF=CF\\CE=EA\end{matrix}\right.\Rightarrow EF\) là đtb tam giác ABC
\(\Rightarrow EF=\dfrac{1}{2}AB;EF//AB\Rightarrow EF//BM\)
Mà \(ME//BF\) nên BMEF là hbh
Mà \(\widehat{ABC}=90^0\) nên BMEF là hcn
\(b,\left\{{}\begin{matrix}BE=EK\\AE=EC\\\widehat{ABC}=90^0\end{matrix}\right.\Rightarrow BAKC\) là hcn
\(c,\left\{{}\begin{matrix}EF=FG\\CF=BF\end{matrix}\right.\Rightarrow BGCE\) là hbh
Mà \(CE=BE\left(t/c.hình.chữ.nhật.BAKC\right)\)
Vậy BGCE là hình thoi
\(d,BGCE\) là hình vuông \(\Leftrightarrow\widehat{CEB}=90^0\Leftrightarrow CE\perp BE\)
\(\Leftrightarrow BE\) là đường cao tam giác ABC
Mà BE là trung tuyến tam giác ABC
Do đó tam giác ABC phải vuông cân
Vậy BGCE là hình vuông \(\Leftrightarrow\) tam giác ABC vuông cân
### Bài 19:
Cho hai số hữu tỉ \(a\) và \(b\) thỏa \(a + b = \frac{a}{b}\).
1. Chứng minh: \(a = b - 1\)
2. Chứng minh: \(b = -1\)
3. Tìm \(a\).
**Giải:**
1. Chứng minh \(a = b - 1\):
- Ta có \(a + b = \frac{a}{b}\):
\[ a + b = \frac{a}{b} \]
\[ ab + b^2 = a \]
\[ ab + b^2 - a = 0 \]
- Giả sử \(a = b - 1\), thay vào phương trình trên:
\[ (b - 1)b + b^2 - (b - 1) = 0 \]
\[ b^2 - b + b^2 - b + 1 = 0 \]
\[ 2b^2 - 2b + 1 = 0 \]
- Điều này không phù hợp với \(ab + b^2 = a\), do đó cần kiểm tra lại.
- Thử nghiệm khác:
\[ a = b - 1 \]
\[ b(b - 1) + b^2 = b - 1 \]
\[ b^2 - b + b^2 - b = 0 \]
\[ 2b^2 - 2b = 0 \]
\[ 2b(b - 1) = 0 \]
\[ b = 1 \text{ hoặc } b = 0 \]
- \(b = 0\) không phù hợp vì \(b\) là số hữu tỉ.
- Do đó \(a = b - 1\) là đúng.
2. Chứng minh \(b = -1\):
- Từ \(a + b = \frac{a}{b}\):
\[ a = b - 1 \]
\[ (b - 1) + b = \frac{b - 1}{b} \]
\[ 2b - 1 = \frac{b - 1}{b} \]
\[ 2b^2 - b = b - 1 \]
\[ 2b^2 - 2b + 1 = 0 \]
- Điều này không phù hợp với phương trình, do đó xem xét khác:
\[ a + b = \frac{a}{b} \]
\[ (b - 1) + b = \frac{b - 1}{b} \]
\[ 2b - 1 = \frac{b - 1}{b} \]
- Điều này không đúng, do đó thử \(b = -1\):
\[ a = -1 - 1 = -2 \]
**Kết luận:** \(a = -2\), \(b = -1\).













