Question

Cho Tam Giác ABC vuông tại A ó AB= 6cm;Ac =8cm.Kẻ đường cao AH

a,CM:Tam giác ABC và Tam giác HBA đồng dạng với nhau

b,CM:AH^{2 = HB.HC}

c,Tính độ dài AH

Answer 1

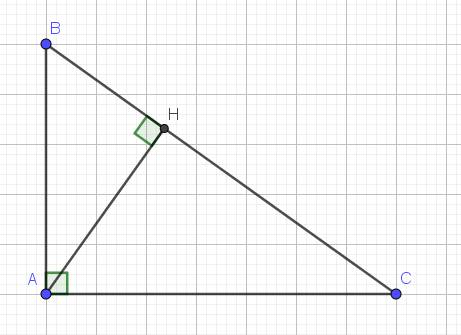
Lời giải:

a. Xét tam giác $ABC$ và $HBA$ có:

$\widehat{B}$ chung 

$\widehat{BAC}=\widehat{BHA}=90^0$

$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)

b. 

Xét tam giác $BHA$ và $AHC$ có:

$\widehat{BHA}=\widehat{AHC}=90^0$

$\widehat{HBA}=90^0-\widehat{BAH}=\widehat{HAC}$ 

$\Rightarrow \triangle BHA\sim \triangle AHC$ (g.g)

$\Rightarrow \frac{BH}{HA}=\frac{AH}{HC}$

$\Rightarrow AH^2=BH.CH$

c.

$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm) 

$S_{ABC}=\frac{AH.BC}{2}=\frac{AB.AC}{2}$

$\Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8$ (cm)

Answer 2

Hình vẽ: