Bạn tham khảo ở hình dưới, thay trung điểm M trong hình thành trung điểm J là ok so với đề nha :)
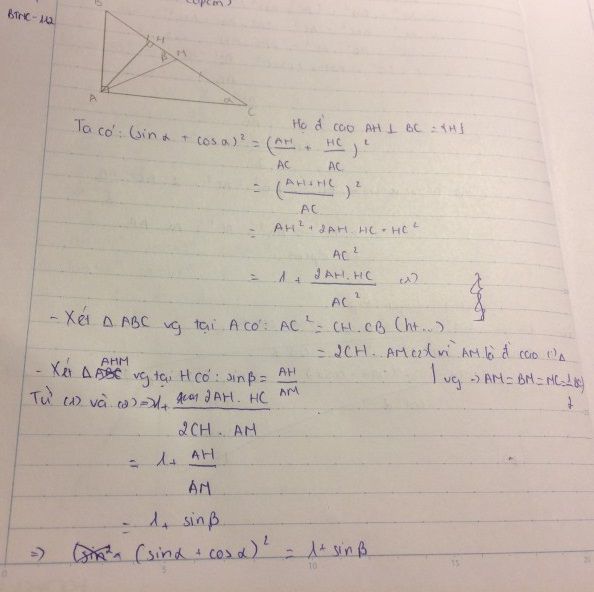
Bạn tham khảo ở hình dưới, thay trung điểm M trong hình thành trung điểm J là ok so với đề nha :)
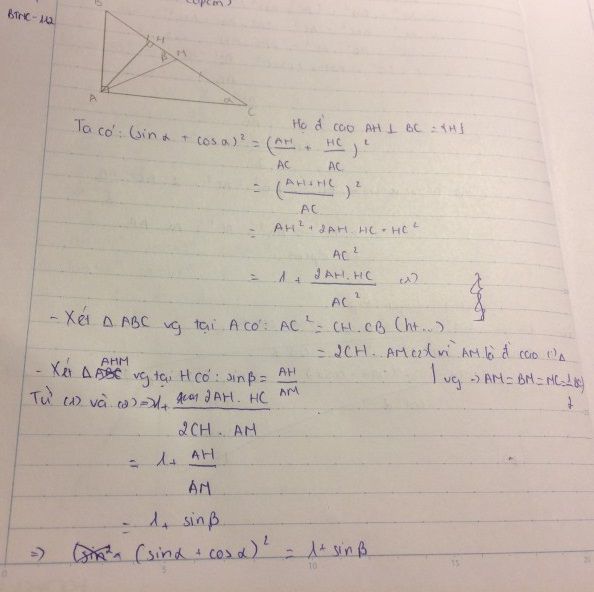
a) \(\cos^2\)α+ \(\cos^2\)β + \(\cos^2\)α.\(\sin^2\)β +\(^{ }\sin^2\)α
b) 2(\(\sin\)α - \(\cos\)α)\(^2\) - ( \(\left(\sin\alpha+\cos\alpha\right)^{2^{ }}+\left(\sin\alpha.\cos\alpha\right)\)
c) \(\left(\tan\alpha-\cot\alpha\right)^2-\left(\tan\alpha+\cos\alpha\right)^2\)
Cho hai góc nhọn α và β thỏa mãn \(0^o\)<α+β<\(90^0\). Chứng minh: cos(α+β)=cosα.cosβ-sinα.sinβ
a) Cho góc α < 90o có sin α = \(\dfrac{1}{3}\). Tính cos α, tg α, ctg α.
b) Cho góc β < 90o có tan β = 2. Tính sin β, cos β.
Biết \(sin\alpha=\dfrac{12}{13};sin\beta=\dfrac{\sqrt{3}}{2}\). Tính các tỉ số lượng giác còn lại của các góc \(\alpha;\beta\)
\(K=\sin^6\alpha+\cos^6\beta+3.\sin^2\alpha.\cos^2\alpha\)
Cho góc nhọn α
a) Rút gọn biểu thức S=\(\cos^2\alpha+tg^2.\cos^2\alpha\)
b) Chứng minh:
\(\dfrac{\left(\sin\alpha+\cos\alpha\right)^2-\left(\sin\alpha-\cos\alpha\right)^2}{\sin\alpha.\cos\alpha}=4\)
Help me plsssssssssss
Xét hình bs 4 :

Tìm đẳng thức đúng :
(A) \(\cos^2\alpha+\sin^2\beta=1\) (B) \(\sin^2\alpha+\cos^2\beta=1\)
(C) \(\sin^2\alpha+\cos^2\alpha=1\) (D) \(\cos^2\alpha+\cos^2\beta=2\)
Bài 3: Cho ∆ABC vuông tại A. AB/BC = 1/2.Tính Sin alpha, Cos alpha, Tân alpha
CMR
a)\(\frac{1+\cos\alpha}{\sin\alpha}=\frac{\sin\alpha}{1-\cos\alpha}\)
b)\(\frac{\tan\alpha+1}{\tan\alpha-1}=\frac{1+\cot\alpha}{1-\cot\alpha}\)
c) \(\tan^2\alpha-\sin^2\alpha=\tan^2\alpha.\sin^2\alpha\)
d)\(\frac{1-4\sin^2\alpha.\cos^2\alpha}{\left(\sin\alpha-\cos\alpha\right)^2}=\left(\sin\alpha+\cos\alpha\right)^2\)