a: Xét ΔABC và ΔECB co
AB=EC
AC=EB
BC chung
Do đó: ΔABC=ΔECB
Xét ΔECB và ΔFCB có
EC=FC
BC chung
EB=FB
Do đó: ΔECB=ΔFCB
b: Xét tứ giác ABFC có
AB=FC
AC=BF
Do đó: ABFC là hình bình hành
=>AC//BF; AB//CF
a: Xét ΔABC và ΔECB co
AB=EC
AC=EB
BC chung
Do đó: ΔABC=ΔECB
Xét ΔECB và ΔFCB có
EC=FC
BC chung
EB=FB
Do đó: ΔECB=ΔFCB
b: Xét tứ giác ABFC có
AB=FC
AC=BF
Do đó: ABFC là hình bình hành
=>AC//BF; AB//CF
Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán kính AB, chúng cắt nhau tại D (D và B nằm khác phía đối với AC). Chứng minh: a. AD // BC b. AB // CD
Cho tam giác ABC. Vẽ đường tròn tâm B bán kính AC, đường tròn tâm C bán kính AB. Hai đường tròn này cắt nhau tại hai điểm E và F thuộc hai nửa mặt phẳng đối nhau bờ là đường thẳng BC. Chứng minh:
a)ΔABC=ΔECB=ΔFCB
b)AB//CF, AC//BF
c)ΔABE=ΔECA
Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán kính BA, chúng cắt nhau tại D ( D và B nằm khác phía đối với AC). Chứng minh rằng AD // BC![]() zúp mik vs ko chép mạng nhaaaaaaaaa
zúp mik vs ko chép mạng nhaaaaaaaaa
Cho đọan thẳng AB dài 4cm. Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 3cm, chúng cắt nhau ở C và D. Chứng minh rằng AB là tia phân giác của góc CAD ?
Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán kính bằng BA, chúng cắt nhau ở D (D và B nằm khác phía đối với AC). Chứng minh rằng AD // BC ?
Cho tam giác ABC. Vẽ đường tròn tâm B bán kính AC, đường tròn tâm C bán kính AB. Hai đường tròn này cắt nhau tại hai điểm E và F thuộc hai nửa mặt phẳng đối nhau bờ là đường thẳng BC. CMR: AE//BC
Cho đoạn thẳng AB. Vẽ cung tròn tâm A bán kính AB và cung tròn tâm B bán kính BA, chúng cắt nhau ở C và D. Chứng minh rằng :
a) \(\Delta ABC=\Delta ABD\)
b) \(\Delta ACD=\Delta BCD\)
Cho góc xOY và tia Am (h.74a)
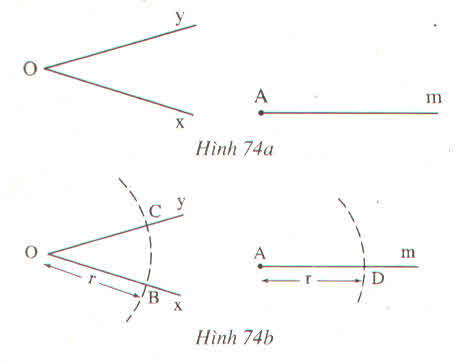
Vẽ cung tròn tâm O bán kính, cung này cắt Ox, Oy theo thứ tự ở B, C. Vẽ cung tròn tâm A bán kính r, cung này cắt tia Am ở D (h.74b)
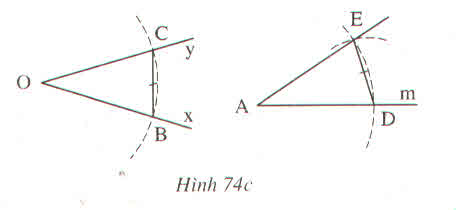
Vẽ cung tròn tâm D có bán kính bằng BC, cung này cắt cung tròn tâm A bán kính r ở E (h.74c)
Chứng minh rằng \(\widehat{DAE}=\widehat{xOy}\) ?
Cho góc xOy (h.73). Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự ở A, B ((1)). Vẽ các cung tròn tâm A và tâm B có cùng bán kính sao cho chúng cắt nhau ở điểm C nằm trong góc xOY ((2), (3)). Nối O với C ((4)). Chứng minh rằng OC là tia phân giác của góc xOy ?
