a: Xét ΔMAB có MI là phân giác
nên AI/IB=AM/MB=AM/MC
Xét ΔAMC có MK là phân giác
nên AK/KC=AM/MC
=>AI/IB=AK/KC
=>IK//BC
b: Xét ΔABM có IO//BM
nên IO/BM=AO/AM
Xét ΔACM có OK//MC
nên OK/MC=AO/AM
=>IO/BM=OK/MC
mà BM=CM
nên IO=OK
a: Xét ΔMAB có MI là phân giác
nên AI/IB=AM/MB=AM/MC
Xét ΔAMC có MK là phân giác
nên AK/KC=AM/MC
=>AI/IB=AK/KC
=>IK//BC
b: Xét ΔABM có IO//BM
nên IO/BM=AO/AM
Xét ΔACM có OK//MC
nên OK/MC=AO/AM
=>IO/BM=OK/MC
mà BM=CM
nên IO=OK
Bài 3:Cho tam giác ABC với trung tuyến AM.Tia phân giác góc AMB cắt cạnh AB tại D,tia phân giác góc AMC cắt cạnh AC tại E.
a)Chứng minh DE và BC song song với nhau.
b)Gọi I là giao điểm của AM,DE.Chứng minh IM=\(\dfrac{1}{2}\)DE.
Cho tam giác ABC với đường trung tuyến AM tia phân giác của góc amb cắt cạnh AB ở D , tia phân giác của góc A MC cắt AC ở E chứngA) DE (AM+MB)=AM.BCB) gia sư AI là tia p.g của góc BẠC (I €BC) và CA =CB=15cm,AB =10cm.ke AK vg góc với AI (k €BC)Tính đô dài đoan KI
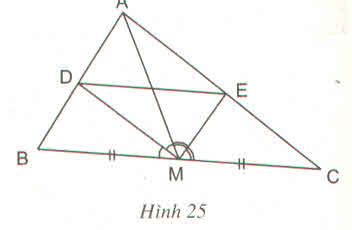
Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC (h.25)
Cho tam giác ABC có AB > AC, BE là phân giác, BD là trung tuyến (E,D thuộc cạnh AC). Đường thẳng qua C vuông góc với BE cắt BE, BD, BA lần lượt tại F, G và K. DF cắt BC tại M. Chứng minh rằng
a) M là trung điểm của đoạn thẳng BC.
b)DA/DE=1+BK/DF
Cho tam giác MNP trung tuyến ME. Các đường phân giác của góc MEN và góc PEM lần lượt cắt các cạnh MN, MP tại C và D a) cmr: CD // NP b) gọi O là giao điểm của ME và CD. Cmr OC= OD
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Gọi BD là đường phân giác của tam giác ABC.
a) Tính độ dài DA, DC.
b) Tia phân giác của góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh \(\widehat{BIM}\) = 90o
Bài 1: Cho tam giác ABC, trung tuyến AM. Đường phân giác của góc AMB cắt cạnh AB ở D, đường phân giác của góc AMC cắt cạnh AC ở E.
a) Chứng minh: DE // BC
b) Gọi I là giao điểm của DE với AM. Chứng minh: ID = IE.
(không cần phải vẽ hình)
4: Cho ABC có đường trung tuyến AM. Đường phân giác của góc AMB cắt
cạnh AB ở E, đường phân giác của góc AMC cắt AC ở F.
a) Chứng minh:
EF // BC
b) Gọi I là giao điểm của EF và AM. Chứng minh I là trung điểm của EF
c) Biết AM = 7 cm, BC = 12 cm. Tính tỉ số diện tích hai tam giác AMF và MFC
d) Kẻ tia FM cắt tia AB tại K. Chứng minh rằng: KB.EA=KA.EB
Cho △ABC có AM là đường trung tuyến. Gọi MS, MQ lần lượt là cácđường phân giác của △AMB , △AMC .a) Chứng minh: SQ // BCb) SC cắt MA, MQ lần lượt ở V, I. Chứng minh: SC.IV = SV. IC c) Chứng minh: BQ đi qua điểm V.