Ôn thi vào 10
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, đường cao AH (H \(\in\) BC). Qua B kẻ đường thẳng vuông góc với BC tại B, cắt AC tại D. Gọi K là hình chiếu của A trên BD. Chứng minh rằng BK.BD = BH.BC, từ đó suy ra \(\Delta\)BHK \(\backsim\) \(\Delta\)BDC
Cho tam giác ABC có cạnh AB AC. Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I đối xứng với H qua D. Gọi M và N lần lượt là hình chiếu vuông góc của I trên AB và AC.a) Chứng minh tứ giác ABDE nội tiếp và góc widehat{CAD}widehat{CBI} ?b) Chứng minh rằng góc widehat{MDI}widehat{ACI} và tam giác ACI đồng dạng với tam giác MDI ?c) Gọi P và Q lần lượt là trung điểm của MD và AC. Chứng minh rằng góc widehat{IPQ}90^0 ?P/s: Nhờ thầy cô và các bạn giúp đỡ ý c với ạ, cám ơn n...
Đọc tiếp
Cho tam giác ABC có cạnh AB < AC. Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I đối xứng với H qua D. Gọi M và N lần lượt là hình chiếu vuông góc của I trên AB và AC.
a) Chứng minh tứ giác ABDE nội tiếp và góc \(\widehat{CAD}=\widehat{CBI}\) ?
b) Chứng minh rằng góc \(\widehat{MDI}=\widehat{ACI}\) và tam giác ACI đồng dạng với tam giác MDI ?
c) Gọi P và Q lần lượt là trung điểm của MD và AC. Chứng minh rằng góc \(\widehat{IPQ}=90^0\) ?
P/s: Nhờ thầy cô và các bạn giúp đỡ ý c với ạ, cám ơn nhiều ạ!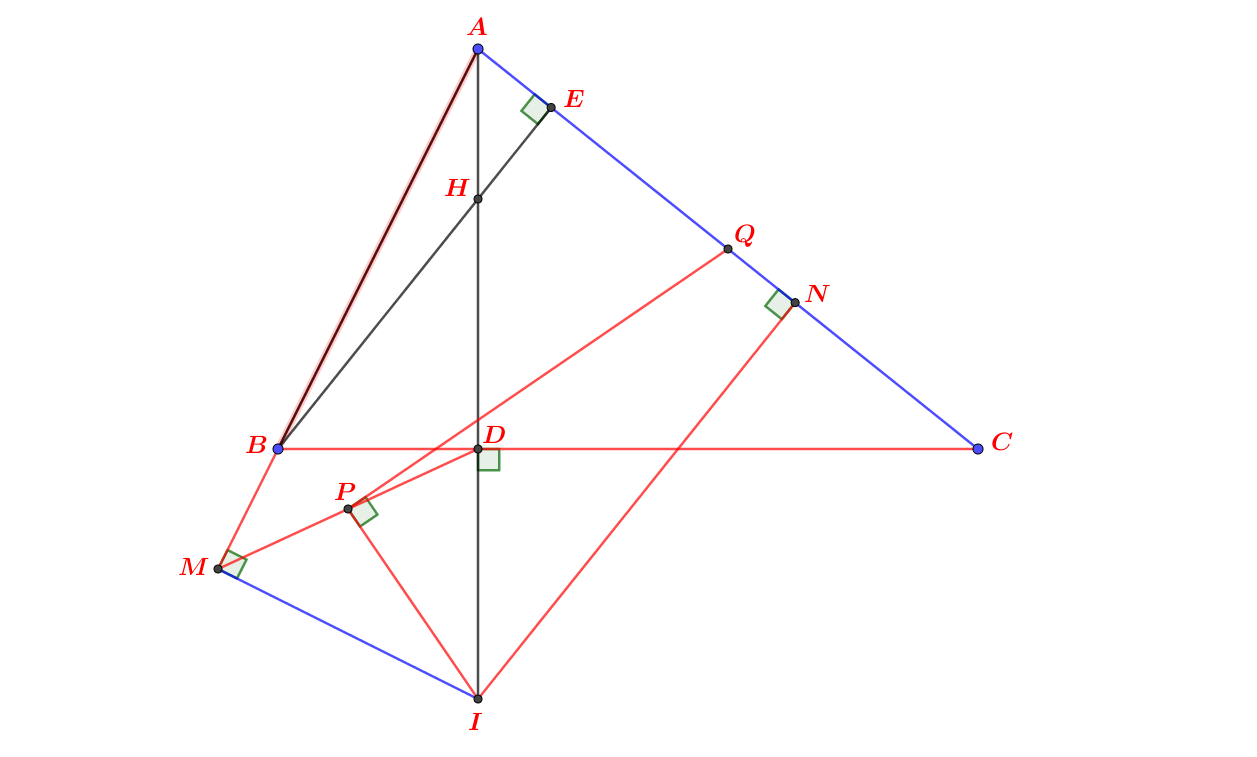
8/79cho tam giác ABC nhọn (ABAC) nội tiếp đường tròn O . tiếp tuyếm tại A của đường tròn O cắt đường thẳng BC tại MA/chứng minh MA2 MB.MCB/vẽ đường cao BD của tam giác ABC , đường thẳng qua D và song song với MA cắt AB tại E . chứng minh CE là đường cao của tam giác ABCc/ gọi N là điểm chính giữa cung nhỏ BC . gọi I và K lần lượt là giao điểm của AN với BD và CE . tìm điều kiện của tam giác ABC để có IB/ID . KC/KE IB/ID+KC/KEthankkkkkkk
Đọc tiếp
8/79
cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn O . tiếp tuyếm tại A của đường tròn O cắt đường thẳng BC tại M
A/chứng minh MA2 = MB.MC
B/vẽ đường cao BD của tam giác ABC , đường thẳng qua D và song song với MA cắt AB tại E . chứng minh CE là đường cao của tam giác ABC
c/ gọi N là điểm chính giữa cung nhỏ BC . gọi I và K lần lượt là giao điểm của AN với BD và CE . tìm điều kiện của tam giác ABC để có IB/ID . KC/KE = IB/ID+KC/KE
thankkkkkkk
Cho ABC có ba góc nhọn nội tiếp đường tròn tâm O (AB AC) và AH là đường cao của tam giác. Gọi M, N lần lượt là hình chiếu vuông góc của H lên AB, AC. Kẻ NE vuông góc với AH. Đường thẳng vuông góc với AC kẻ từ C cắt tia AH tại D và AD cắt đường tròn tại F. Chứng minh : a) ABC + ACB BIC và tứ giác DENC nội tiếp;b) AM.AB AN.AC và tứ giác BFIC là hình thang cân;c) Tứ giác BMED nội tiếp.
Đọc tiếp
Cho ABC có ba góc nhọn nội tiếp đường tròn tâm O (AB < AC) và AH là đường cao của tam giác. Gọi M, N lần lượt là hình chiếu vuông góc của H lên AB, AC. Kẻ NE vuông góc với AH. Đường thẳng vuông góc với AC kẻ từ C cắt tia AH tại D và AD cắt đường tròn tại F. Chứng minh :
a) ABC + ACB = BIC và tứ giác DENC nội tiếp;
b) AM.AB = AN.AC và tứ giác BFIC là hình thang cân;
c) Tứ giác BMED nội tiếp.
Cho (O) qua điểm A nằm ngoài đường tròn,kẻ tiếp tuyến AB và AC với đường tròn.(BC là tiếp điểm).Kể đường kính BD,đường thẳng DC cắt BA tại E,AO cắt BC tại H,đường thẳng qua C và vuông góc với BD cắt AD tại K. Chứng minh rằng : a) AO vuông góc với BC b) AB = AE c) HK // BD
Cho (O) qua điểm A nằm ngoài đường tròn,kẻ tiếp tuyến AB và AC với đường tròn.(BC là tiếp điểm).Kể đường kính BD,đường thẳng DC cắt BA tại E,AO cắt BC tại H,đường thẳng qua C và vuông góc với BD cắt AD tại K. Chứng minh rằng AB = AE
Cho (O) qua điểm A nằm ngoài đường tròn,kẻ tiếp tuyến AB và AC với đường tròn.(BC là tiếp điểm).Kể đường kính BD,đường thẳng DC cắt BA tại E,AO cắt BC tại H,đường thẳng qua C và vuông góc với BD cắt AD tại K. Chứng minh rằng AB = AE
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R), ba đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm đối xứng với H qua BC.a)Chứng minh: Tứ giác ACKB nội tiếp.b)Kẻ đường kính AA của (O). C/m AA⊥⊥EF.c)Gọi I là trung điểm BC. C/m ba điểm H, I, A thẳng hàng.d)Gọi G là trọng tâm tâm tam giác ABC. C/m SAHG2SAOGchứng minh ghi rõ nha
Đọc tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R), ba đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm đối xứng với H qua BC.
a)Chứng minh: Tứ giác ACKB nội tiếp.
b)Kẻ đường kính AA' của (O). C/m AA'⊥⊥EF.
c)Gọi I là trung điểm BC. C/m ba điểm H, I, A' thẳng hàng.
d)Gọi G là trọng tâm tâm tam giác ABC. C/m SAHG=2SAOG
chứng minh ghi rõ nha
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R), ba đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm đối xứng với H qua BC.a)Chứng minh: Tứ giác ACKB nội tiếp.b)Kẻ đường kính AA của (O). C/m AAperpEF.c)Gọi I là trung điểm BC. C/m ba điểm H, I, A thẳng hàng.d)Gọi G là trọng tâm tâm tam giác ABC. C/m S_{AHG}2S_{AOG}
Đọc tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R), ba đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm đối xứng với H qua BC.
a)Chứng minh: Tứ giác ACKB nội tiếp.
b)Kẻ đường kính AA' của (O). C/m AA'\(\perp\)EF.
c)Gọi I là trung điểm BC. C/m ba điểm H, I, A' thẳng hàng.
d)Gọi G là trọng tâm tâm tam giác ABC. C/m \(S_{AHG}=2S_{AOG}\)









