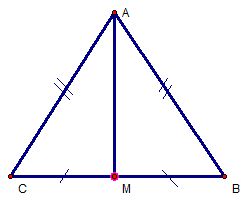
a) Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:
\(AB=AC\left(gt\right)\)
\(BM=CM\) (vì M là trung điểm của \(BC\))
Cạnh AM chung
=> \(\Delta ABM=\Delta ACM\left(c-c-c\right)\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> \(AM\) là đường phân giác của \(\widehat{A}.\)
b) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
Có \(AM\) là đường phân giác (cmt) đồng thời \(AM\) cũng là đường cao của \(\Delta ABC.\)
=> \(AM\) là đường cao của \(\Delta ABC.\)
c) Theo câu b) ta có \(\Delta ABC\) cân tại A.
Có \(AM\) là đường cao đồng thời \(AM\) cũng là đường trung trực của \(\Delta ABC.\)
=> \(AM\) là đường trung trực của \(BC.\)
Chúc bạn học tốt!










