Question

Cho tam giác ABC có AB = AC . Chứng minh góc C = góc B

a , bằng cách gọi M là trung điểm của BC

b , bằng cách khác tùy thích

Cho tam giác ABC , trên nửa mặt phẳng bờ AC không chứa điểm B , vẽ điểm D sao cho AD = BC và CD = AB . CMR AB song song CD và AD // BC

Answer 1

1,

a) Gọi M là trung điểm của BC

\(\Rightarrow MB=MC\)

Xét △AMB và △AMC có:

\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\MB=MC\left(cmt\right)\\AM:\text{cạnh chung}\end{matrix}\right.\)

\(\Rightarrow\) △AMB = △AMC (c.c.c)

b) Kẻ AD là tia phân giác của \(\widehat{BAC}\)

\(\Rightarrow\widehat{BAD}=\widehat{DAC}\)

Xét △ADB và △ADC có:

\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{BAD}=\widehat{DAC}\left(cmt\right)\\AD:\text{cạnh chung}\end{matrix}\right.\)

\(\Rightarrow\) △ADB = △ADC (c.g.c)

Answer 2

a)

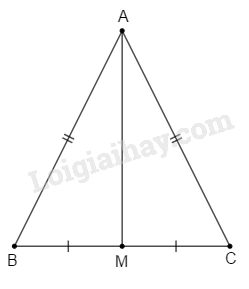
Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:

\(AB=AC\left(gt\right)\)

\(BM=CM\) (vì M là trung điểm của \(BC\))

Cạnh AM chung

=> \(\Delta ABM=\Delta ACM\left(c-c-c\right).\)

=> \(\widehat{ABM}=\widehat{ACM}\) (2 góc tương ứng).

Hay \(\widehat{ABC}=\widehat{ACB}.\)

b) Cách khác:

Xét \(\Delta ABC\) có:

\(AB=AC\left(gt\right)\)

=> \(\Delta ABC\) cân tại A.

=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân)

Bài 2:

Xét 2 \(\Delta\) \(CDA\) và \(ABC\) có:

\(CD=AB\left(gt\right)\)

\(DA=BC\left(gt\right)\)

Cạnh AC chung

=> \(\Delta CDA=\Delta ABC\left(c-c-c\right)\)

=> \(\widehat{DAC}=\widehat{BCA}\) (2 góc tương ứng)

Mà 2 góc này nằm ở vị trí so le trong.

=> \(AD\) // \(BC\left(đpcm1\right).\)

Vì \(\Delta CDA=\Delta ABC\left(cmt\right)\)

=> \(\widehat{DCA}=\widehat{BAC}\) (2 góc tương ứng)

Mà 2 góc này nằm ở vị trí so le trong.

=> \(AB\) // \(CD\left(đpcm2\right).\)

Chúc bạn học tốt!