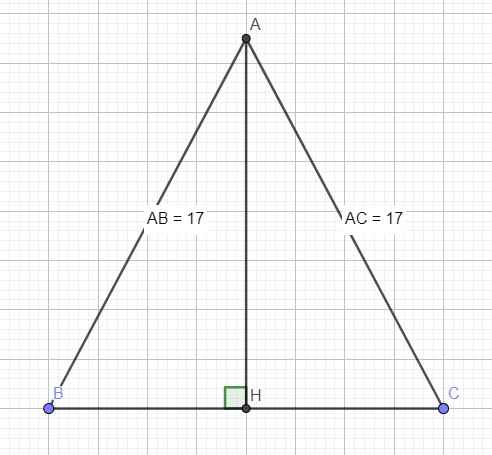
Do tam giác ABC cân tại A nên AH là đường cao đồng thời là trung tuyến
\(\Rightarrow\) H là trung điểm BC \(\Rightarrow BH=CH=\dfrac{1}{2}BC=8\)
Áp dụng định lý Pitago cho tam giác vuông ABH:
\(AH=\sqrt{AB^2-BH^2}=15\)
\(cosB=\dfrac{BH}{AB}=\dfrac{8}{17}\Rightarrow B\approx62^0\) \(\Rightarrow C=B=62^0\)
\(\Rightarrow A=180^0-\left(B+C\right)=56^0\)
Cho tam giác ABC vuông tại A,đường cao AH, trung tuyến AM, AB = 4cm, sinB=1/3 a. Tình AC,BC,AH b. Tính cos góc MAH
Cho tam giác ABC vuông tại A có đường cao AH,
AB = 15 cm và BH = 9 cm.
a/ Tính BC và AC.
b/ Tính góc HAC (số đo góc làm tròn đến phút).
c/ Tia phân giác của góc ABC cắt AH và AC tại F, E.
Chứng minh : BC = EC . tan(AFE)
Cho tam giác ABC vuông tại A, đường cao AH, AH =2cm, góc ACB = 30 độ. Tính AC và AB
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 9; góc B = 500. Giải tam giác ABC và tính đường cao AH?
cho tam giác ABC vuông tại A, đường cao AH. Gọi D,E là hình chiếu vuông góc của H trên AB,AC. Tính số đo các góc của tam giác HDE. Biết \(\dfrac{DE}{BC}\)\(=\dfrac{\sqrt{3}}{4}\)
Cho tam giác ABC cân tại A . Góc A =120°, BC =2, BH vuông góc với AC ( H thuộc AC) . Tính AH
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HM vuông góc AB, HN vuông góc AC. CMR;
a) AN.AC=HB.HC
b) AB²/AC²=BH/HC
c) AH²+BH²=BH.BC
Cho tam giác ABC vuông tại A, AH vuông góc với BC,có AH=2, tan B=1/3. Tính AB, AC. Mong mn giúp mình
Cho tam giác ABC vuông tại A, có đường cao AH.
a) Biết AH=4cm, CH=2cm, Tính AB, AC.
b) Từ H vẽ HD vuông góc với AB tại D, HE vuông góc với AC tại E.
CM: AD.AB-AE.AC
c) CM: DE\(^3\)-BD.CE.BC
