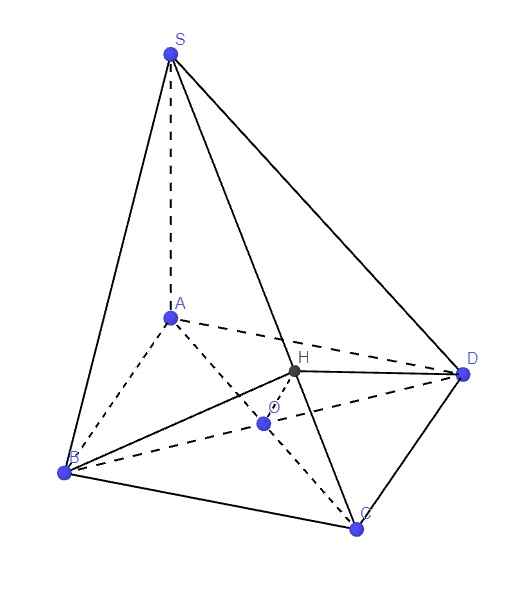
Gọi O là tâm đáy, từ O kẻ \(OH\perp SC\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\) \(\Rightarrow BD\perp SC\)
\(\Rightarrow SC\perp\left(BDH\right)\Rightarrow\left\{{}\begin{matrix}SC\perp BH\\SC\perp DH\end{matrix}\right.\) góc giữa BH và DH là góc \(\alpha\) giữa (SCD) và (SBC)
\(BD=a\sqrt{2}\) ; \(SB=SD=a\sqrt{2}\)
Hệ thức lượng trong tam giác vuông SBC:
\(BH=\dfrac{SB.BC}{\sqrt{SB^2+BC^2}}=\dfrac{a\sqrt{6}}{3}\), tương tự \(DH=\dfrac{a\sqrt{6}}{3}\)
\(\Rightarrow cos\alpha=\left|cos\widehat{BHD}\right|=\left|\dfrac{BH^2+DH^2-BD^2}{2BH.DH}\right|=\dfrac{1}{2}\)
\(\Rightarrow\alpha=60^0\)