Bài 10: Diện tích hình tròn
Các câu hỏi tương tự
Cho (O,R) vẽ 2 đường kính AC Và BD vuông góc với nhau. Vẽ đường tròn (B,BA) qua A và C
Tính A hình trăng lưỡi liềm ADCA biết R=10cm , π gần = 3,14
Giúp em với mn
Cho tam giác ABC vuông ở A và đường cao AH. Vẽ đường tròn tâm O đường kính AB. Biết BH = 2cm, HC = 6cm. Tính :
a) Diện tích hình tròn (O)
b) Tổng diện tích hai hình viên phân AmH và BnH (ứng với các cung nhỏ)
c) Diện tích hình quạt tròn AOH (ứng với cung nhỏ AH)
27 tháng 3 2022 lúc 20:50
1. Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R = 3cm. Tính diện tích hình quạt tạo bởi hai bán kính OB,OC và cung nhỏ BC khi \(\widehat{BAC}=60^o\)
2. Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm nội tiếp đường tròn (O). Tính diện tích hình tròn (O)
Cho đường tròn (O; R). Chia đường tròn này thành ba cung có số đo tỉ lệ với 3, 4 và 5 rồi tính diện tích các hình quạt tròn được tạo thành ?
27 tháng 3 2022 lúc 21:48
Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R = 3cm. Tính diện tích hình tròn giới hạn tạo bởi hai bán kính OB,OC và cung nhỏ BC khi \(\widehat{BAC}=60^0\)
Cho ∆ABC nhọn nội tiếp (O,R) có góc BAC 60°. a) Tính diện tích hình viên phân giới hạn bởi cung nhỏ BC và dây BC theo R? b) vẽ BD,CE là hậu đường cao của ∆ABC ( D € AC, E € AB). Chứng minh BEDC nội tiếp và chứng minh: S∆abc4×S ade . c) Gọi M là giáo điểm của BD với (O) ( M khác B). Từ M vẽ MP vuông góc với BC tại P, MQ vuông tại AB tại Q. Chứng minh : ba điểm P,D,Q thẳng hàng
Đọc tiếp
Cho ∆ABC nhọn nội tiếp (O,R) có góc BAC= 60°. a) Tính diện tích hình viên phân giới hạn bởi cung nhỏ BC và dây BC theo R? b) vẽ BD,CE là hậu đường cao của ∆ABC ( D € AC, E € AB). Chứng minh BEDC nội tiếp và chứng minh: S∆abc=4×S ade . c) Gọi M là giáo điểm của BD với (O) ( M khác B). Từ M vẽ MP vuông góc với BC tại P, MQ vuông tại AB tại Q. Chứng minh : ba điểm P,D,Q thẳng hàng
cho đường tròn O đường kính AA'=2R.một dây cung BC vuông góc bán kính OA' tại trung điểm H của OA' a)chứng minh rằng tam giác OBA' và tam giác ABC là các tam giác đều.Tính cạnh tam giác ABC b)đường BO cắt đường tròn O tại D đường DH cắt đường tròn tại M.Tính DH;DM c)tính diện tích tam giác HMC
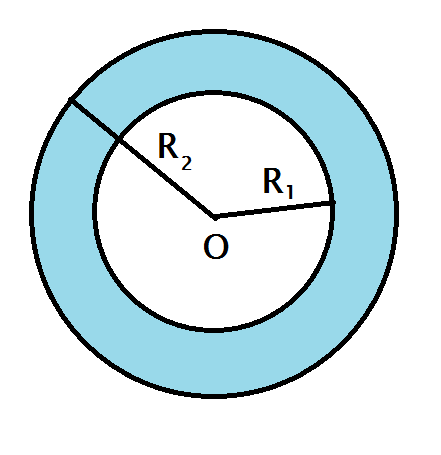
Hình vành khăn là phần hình tròn nằm giữa hai đường tròn đồng tâm.
a) Tính diện tích S của hình vành khăn theo R1 và R2 (giả sử R1 và R2).
b) Tính diện tích hình vành khăn khi R1 = 10,5 cm, R2 = 7,8 cm.
Lấy cạnh BC của một tam giác đều làm đường kính, vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng BC. Cho biết cạnh BC = a, hãy tính diện tích của hai hình viên phân được tạo thành.