Question

Cho mạch điện như hình vẽ: Hiệu điện thế giữa hai điểm B, D không đổi khi mở và đóng khoá K, vôn kế lần lượt chỉ hai giá trị U1 và U2. Biết rằng R2 = 4R1 và vôn kế có điện trở rất lớn. Tính hiệu điện thế giữa hai đầu B, D theo U1 và U2.

 

Answer 1

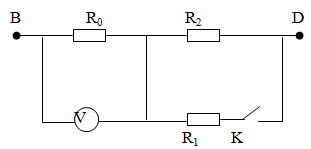
TH1: K mở =>R0 nt R2

\(=>U1=I0.R0\left(V\right)\)

\(=>Ubd=I0.Rtd=\dfrac{U1}{R0}\left(R0+R2\right)=>Ubd=U1+\dfrac{U1.R2}{R0}\)

\(=>\dfrac{U1.R2}{R0}=Ubd-U1=>R0=\dfrac{U1.R2}{Ubd-U1}\)

Th2: R0 nt (R1//R2)

\(=>U0=U2\)

\(=>Ubd=U2+I0.R12=U2+\dfrac{U2}{R0}.\dfrac{R1.R2}{R1+R2}\)

\(=>Ubd=U2+\dfrac{U2}{R0}.\dfrac{\dfrac{R2}{4}.R2}{\dfrac{R2}{4}+R2}=U2+\dfrac{U2}{R0}.\dfrac{\dfrac{R2^2}{4}}{\dfrac{5R2}{4}}\)

\(=U2+\dfrac{U2}{R0}.\dfrac{R2}{5}=>Ubd=U2+\dfrac{U2.R2}{5R0}\)

\(=>R0=\dfrac{U2.R2}{5\left(Ubd-U2\right)}\)

\(=>\dfrac{U1.R2}{Ubd-U1}=\dfrac{U2.R2}{5\left(Ubd-U2\right)}\)

\(=>Ubd=\dfrac{4U1U2}{5U1-U2}\)