a: Xét ΔADE và ΔBDE có
DA=DB
DE chung
AE=BE
Do đó: ΔADE=ΔBDE
Đúng 0
Bình luận (0)
Bài 3: Trường hợp bằng nhau thứ nhất của tam giác canh - cạnh - cạnh (c.c.c)
Các câu hỏi tương tự
Cho hình vẽ bên: a) Chứng minh: tam giác OCB tam gíác ODE b) Chứng minh: góc B góc E c) Chứng minh: BC // DE C B O D E
Đọc tiếp
Cho hình vẽ bên: a) Chứng minh: tam giác OCB = tam gíác ODE
b) Chứng minh: góc B = góc E
c) Chứng minh: BC // DE 
Cho hình 72, chứng minh rằng :
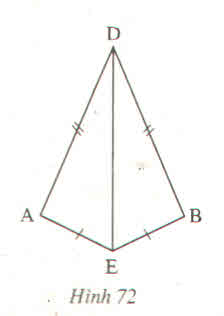
a) \(\Delta ADE=\Delta BDE\)
b) \(\widehat{DAE}=\widehat{DBE}\)
Bài 3. Cho hình vẽ bên. Chứng minh rằng a) ACB ACD b) AC là tia phân giác của góc BAD
Cho tam giác ABC ( AB < AC ) có 0 35 ˆ C = ; B C ˆ 2 ˆ = . Trên tia đối của tia AB lấy điểm D sao cho AD = AB, trên tia đối của tia AC lấy điểm E sao cho AE = AC. a) Tính số đo góc A và góc B của ABC b) Chứng minh: ABC = ADE c) Từ A kẻ AH vuông góc với DE và AK vuông góc với BC ( H DE, K BC). Chứng minh: A là trung điểm của đoạn thẳng HK.
Cho tam giác ABC,góc A =90độ. Trên BC lấy E sao cho BE=BA. Tia phân giác của góc B cắt AC ở D chứng minh rằng:
a) tam giác ABD= tam giác EBD
b) tính số đo góc BED
c) BD vuông góc AE
Xem chi tiết
cho tam giác ABC có AB=AC . Điểm D,E thuộc cạnh BC sao cho BD=DE=EC . Biết AD=AE
a.chứng minh góc EAB=góc DAC
b, gọi m là trung điểm của BC, chứng minh AM là phân giác của DAE
c,Biết DAE =60 độ . tính góc ADE ,góc AED
Cho tam giác ABC có góc A bằng 90 độ , M là trung điểm của AB . Trên tia Cm lấy điểm N sao cho MN=MC
Chứng minh rằng A) tam giác ACM=tam giác BCM B) NB vuông góc với AB C) AN = BC , AN //BC
Vẽ hình hộ
Xem chi tiết
Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OD = OC. Vẽ các cung tròn tâm C và tâm D có cùng bán kính sao cho chúng cắt nhau ở điểm E nằm trong góc xOy. Chứng minh rằng OE là tia phân giác của góc xOy ?
Cho hình vẽ bên,biết EA EB; FA FB; QA QB.a) Vẽ lại hình và viết giả thiết, kết luận;b) Chứng minh ∆AEF ∆BEFc) Chứng minh ∆AEQ ∆BEQ;d) Chứng minh EQ là tia phân giác của góc AEB.
Đọc tiếp
Cho hình vẽ bên,biết EA = EB; FA = FB; QA = QB.
a) Vẽ lại hình và viết giả thiết, kết luận;
b) Chứng minh ∆AEF = ∆BEF
c) Chứng minh ∆AEQ = ∆BEQ;
d) Chứng minh EQ là tia phân giác của góc AEB.