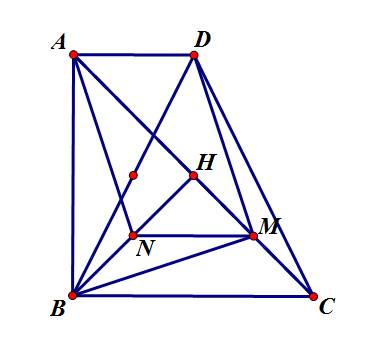
- Bổ sung: \(AD=a\)
- ΔABC có: \(\widehat{BAC}=90^0\), \(AB=BC\).
\(\Rightarrow\)ΔABC vuông cân tại B.
\(\Rightarrow BH=AH=CH=\dfrac{1}{2}AC\);
\(\widehat{ABH}=\widehat{CBH}=\widehat{BAH}=\widehat{CAH}=45^0\)
*Gọi N là trung điểm BH \(\Rightarrow BN=CM\left(=\dfrac{1}{2}BH\right)\)
- ΔHBC có: M,N lần lượt là trung điểm CH,BH.
\(\Rightarrow\)MN là đường trung bình của ΔHBC.
\(\Rightarrow MN=\dfrac{BC}{2}\), MN//BC.
\(\Rightarrow MN=AD\), MN//AD
- Tứ giác ADMN có: \(MN=AD\), MN//AD.
\(\Rightarrow\)ADMN là hình bình hành.
\(\Rightarrow\widehat{DMN}=\widehat{DAN}\left(1\right)\)
- ΔABN và ΔBCM có:
\(\widehat{ABN}=\widehat{BCN}=45^0\)
\(AB=BC\)
\(BN=CM\)
\(\Rightarrow\)ΔABN=ΔBCN (c-g-c).
\(\Rightarrow\widehat{BAN}=\widehat{CBM}\)
Mà \(\widehat{CBM}=\widehat{BMN}\) nên \(\widehat{BAN}=\widehat{BMN}\left(2\right)\)
(1), (2) \(\Rightarrow\widehat{BMN}+\widehat{DMN}=\widehat{DAN}+\widehat{BAN}\)
\(\Rightarrow\widehat{DMB}=90^0\) nên ΔDMB nội tiếp đường tròn đường kính BD.
- Tâm đường tròn ngoại tiếp của ΔDMB là trung điểm BD.
- ΔABD vuông tại A có:
\(BD^2=AD^2+AB^2\)
\(\Rightarrow BD=\sqrt{AB^2+AD^2}=\sqrt{4a^2+a^2}=a\sqrt{5}\)
- Vậy bán kính đường tròn ngoại tiếp ΔDMB là \(\dfrac{a\sqrt{5}}{2}\)













