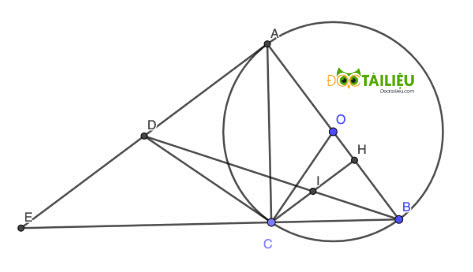
Cho đường tròn tâm O, bán kính R có đường kính AB cố định. C là một điểm thay đổi trên đường tròn (C khác A và B). Gọi H là hình chiếu của C trên AB, I là trung điểm của AC. Đường thẳng OI cắt tiếp tuyến tại A của đường tròn (O;R) tại M, đường thẳng MB cắt đường thẳng CH tại K. Chứng minh IK song song với AB
Gọi E là giao điểm của CB và AM
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC⊥EB tại C
=>ΔACE vuông tại C
ΔOAC cân tại O
mà OI là đường trung tuyến
nên OI là phân giác của góc AOC
Xét ΔOAM và ΔOCM có
OA=OC
\(\hat{AOM}=\hat{COM}\)
OM chung
Do đó: ΔOAM=ΔOCM
=>MA=MC
=>ΔMAC cân tại M
Ta có: \(\hat{MAC}+\hat{MEC}=90^0\) (ΔACE vuông tại C)
\(\hat{MCA}+\hat{MCE}=\hat{ACE}=90^0\)
mà \(\hat{MAC}=\hat{MCA}\)
nên \(\hat{MCE}=\hat{MEC}\)
=>MC=ME
mà MA=MC
nên MA=ME(1)
Xét ΔBMA có HK//AM
nên \(\frac{HK}{AM}=\frac{BK}{BM}\) (2)
Xét ΔBME có CK//ME
nên \(\frac{CK}{ME}=\frac{BK}{BM}\) (3)
Từ (1),(2),(3) suy ra CK=KH
=>K là trung điểm của CH
Xét ΔCAH có
I,K lần lượt là trung điểm của CA,CH
=>IK là đường trung bình của ΔCAH
=>IK//AH
=>IK//AB