Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
Cho hình thang ABCD (AB//CD và AB<CD).Gọi trung điểm của các đường chéo AC và BD thứ tự là N và M.CMR:
a)MN//AB
b)MN=CD-AB/2
cho hình thang ABCD (AB // CD , AB<CD). Gọi trung điểm của AC,BD theo thứ tự M và N. CMR
a, MN // AB
b. \(MN=\dfrac{CD-AB}{2}\)
Cho hình thang ABCD (AB //CD, AB < CD). Gọi trung điểm của các đường chéo AC, BD thứ tự là N và M (h.12).
Chứng minh rằng :
a) MN //AB
b) \(M=\dfrac{CD-AB}{2}\)
Hình thang cân ABCD (AB //CD) có hai đường chéo AC và BD cắt nhau tại O 9h.11).
Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3OM, đáy lớn CD = 5,6 cm
a) Tính độ dài đoạn thẳng MN và đáy nhỏ AB
b) So sánh độ dài đoạn thẳng MN với nửa hiệu các độ dài của CD và AB
Cho hình thang ABCD (AB//CD) gọi O là giao điểm của hai đường chéo. qua O vẽ đường thẳng song song với AB cắt AD và BC Theo thứ tự ở M và N biết AB=6cm CD =10cm Độ dài đoạn thẳng MN là
Cho hình thang ABCD đáy AB và CD (AB<CD) gọi O là giao điểm hai đường chéo m là giao điểm da và CB đường thẳng MO cắt AB và CD thứ tự ở N và K
a, cm AN. KC = BN . KD
b, cm N và K là trung điểm của AB và CD.
Cho hình thang ABCD (AB //CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q chứng minh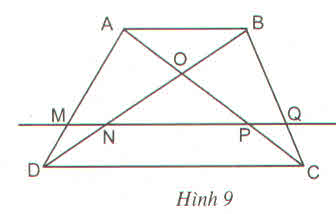 
DN\BD=CP\AC
cho hinh thang abcd (ab//cd ,ab<cd) goi trung diem cua cac duong cheo AC,BD theo thu tu la N va M CMR a) Mn//AB b) MN=(cd-ab) :2
5 tháng 2 2023 lúc 22:38
Cho hình thang ABCD (AB//CD), M là trung điểm CD. I là giao điểm của AM và BD, K là giao điểm của BM và AC.
a) CMR IK // AB
b) Đường thẳng IK cắt AD, BC theo thứ tự ở E, F. CMR EI = IK = KF