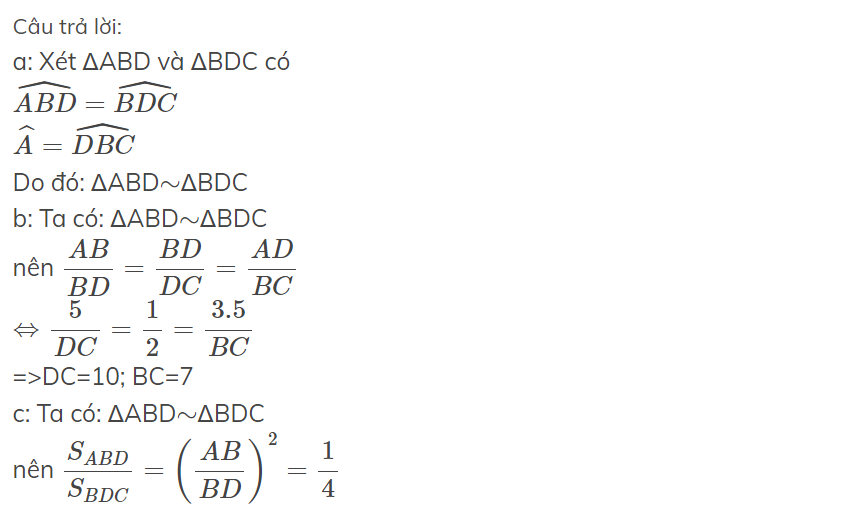Ôn tập toán 8
Các câu hỏi tương tự
Cho hình thang ABCD (AB//CD và góc DAB=góc DBC)biết AB=2,5 cm ; AD=3,5 cm ; BD=5cm
a) Chứng minh ; tam giác ABD đồng dạng với tam giác BDC.
b) Tính độ dài các cạnh BC và CD.
c) Chứng minh :\(\frac{SABC}{SBDC}=\frac{1}{4}\)
1.Cho tam giác đều BSC, phía trong tam giác vẽ tam giác vuông cân ABC.trong tam giác abc lấy điểm D sao cho góc DBC=ACD=30 độ. Chứng minh tứ giác SADC là hình thang
2.Cho hình thang vuông ABCD (góc C=B=90 độ). Có AB=Bc=1/2 DC. Lấy điểm M bất kì trên cạnh AB, lấy điểm N trên cạnh AD sao cho góc NMC=90 độ. Chứng minh rằng khi M thay đổi trên cạnh AB thì góc MNC có số đo không đổi.
Giúp mình với, mình cảm ơn nhiều
B1: Cho hình thang ABCD (AB//CD). Các tia phân giác của góc A và góc B cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng CD=AD+BC
B2: Cho tam giác ABC vuông tại A. Trên nửa mặt phẳng bờ BC ko chứa đỉnh A vẽ BD vuông góc BC và BD=BC
a) Tứ giác ABCD là hình gì? vì sao?
b)Biết AB=5cm. tính CD
Giúp mình với,giải chi tiết cho mình nha!Bài 2: Cho hình thang ABCD (AB//CD).Gọi E,F lần lượt là trung điểm của AD và BC. Gọi K là giao điểm của AC và EFa. CM: AK KC.b. Biết AB 4cm, CD 10cm. Tính các độ dài EK, KFBài 3. Cho tam giác ABC. Gọi D, M, E theo thứ tự là trung điểm của AB, BC, CA.a. CM: Tứ giác ADME là hình bình hành.b. Nếu tam giác ABC cân tại A thì tứ giác ADME là hình gì? Vì sao?c. Nếu tam giác ABC vuông tại A thì tứ giác ADME là hình gì? Vì sao?d. Trong trường hợp tam giác ABC v...
Đọc tiếp
Giúp mình với,giải chi tiết cho mình nha!
Bài 2: Cho hình thang ABCD (AB//CD).Gọi E,F lần lượt là trung điểm của AD và BC. Gọi K là giao điểm của AC và EF
a. CM: AK = KC.
b. Biết AB = 4cm, CD = 10cm. Tính các độ dài EK, KF
Bài 3. Cho tam giác ABC. Gọi D, M, E theo thứ tự là trung điểm của AB, BC, CA.
a. CM: Tứ giác ADME là hình bình hành.
b. Nếu tam giác ABC cân tại A thì tứ giác ADME là hình gì? Vì sao?
c. Nếu tam giác ABC vuông tại A thì tứ giác ADME là hình gì? Vì sao?
d. Trong trường hợp tam giác ABC vuông tại A, cho biết AB = 6cm, AC = 8cm, tính độ
dài AM.
Bài 4: Cho hình bình hành ABCD có AD = 2AB, Ẩ = 60°. Gọi E và F lần lượt là trung
điểm của BC và AD.
a. Chứng minh AE vuông góc BF
b. Chứng minh tứ giác BFDC là hình thang cân.
c. Lấy điểm M đối xứng của A qua B. Chứng minh tứ giác BMCD là hình chữ nhật.
d. Chứng minh M, E, D thẳng hàng.
Bài 5: Cho tam giác ABC vuông tại A có góc ABC= 60°, kẻ tia Ax song song với BC.
Trên Ax lấy điểm D sao cho AD = DC.
a. Tính các góc BAD và DAC.
b. Chứng minh tứ giác ABCD là hình thang cân.
c. Gọi E là trung điểm của BC. Chứng minh tứ giác ADEB là hình thoi.
d. Cho AC = 8cm, AB = 5cm. Tính diện tích hình thoi ABED
BÀI 1:Chứng minh rằng nếu hai cạnh bên của một hình thang cắt nhau thì đường thẳng đi qua giao điểm đó và giao điểm 2 đường chéo sẽ đi qua trung điểm các đáy của hình thang.BÀI 2:Tam giác ABC có BC 2AB và góc ABC120 độ. Chứng minh rằng đường trung tuyến BM vuông góc ABBÀI 3:Cho tam giác ABC vuông tại A. về phía ngoài tam giác lấy AB và BC làm cạnh, dựng các hình vuông ABDE và BCFG. Chứng minh GA vuông góc CDBÀI 4:Trên 2 cạnh AB và AC của tam giác ABC ta dựng ra phía ngoài của tam giác các hình v...
Đọc tiếp
BÀI 1:
Chứng minh rằng nếu hai cạnh bên của một hình thang cắt nhau thì đường thẳng đi qua giao điểm đó và giao điểm 2 đường chéo sẽ đi qua trung điểm các đáy của hình thang.
BÀI 2:
Tam giác ABC có BC= 2AB và góc ABC=120 độ. Chứng minh rằng đường trung tuyến BM vuông góc AB
BÀI 3:
Cho tam giác ABC vuông tại A. về phía ngoài tam giác lấy AB và BC làm cạnh, dựng các hình vuông ABDE và BCFG. Chứng minh GA vuông góc CD
BÀI 4:
Trên 2 cạnh AB và AC của tam giác ABC ta dựng ra phía ngoài của tam giác các hình vuông ABDE và ACFG ; dựng hình bình hành AEHG. Gọi K là giao điểm của AD và BE . Chứng minh CK vuông góc KH
Bài 1:Cho tam giác ABC cân tại A, các đường phân giác BD,CE ( D ϵ AC , E ϵ AB ). Chứng minh rằng BEDC là hình thang có đáy nhỏ bằng cạnh bên.
Bài 2: Hình thang ABCD ( AB II CD ) có góc ACD = góc BDC. Chứng minh rằng ABCD là hình thang cân
1.Cho tam giác ABC cân tại A góc A 108 độ .Vẽ tia phân giác AD và BE : chứng minh AD 1/2 BE2. Chọ hình thang ABCD , AB CD,AB // CD .M là trung điểm của AB . Kẻ MH // AD ( H thuộc BD). Kẻ MK // BC (K thuộc AC).KE dường thẳng đi qua H và vuông góc với MH.Đường thẳng đi qua K và vuông góc với MK .Hai đường thẳng đó cắt nhau tại I.Chứng minhMÌNH MỚI HỌC ĐƯỜNG TRUNG BÌNH CỦA HÌNH THANG VÀ TAM GIÁC . GIÚP MÌNH NHÉ !
Đọc tiếp
1.Cho tam giác ABC cân tại A góc A = 108 độ .Vẽ tia phân giác AD và BE : chứng minh AD = 1/2 BE
2. Chọ hình thang ABCD , AB < CD,AB // CD .M là trung điểm của AB . Kẻ MH // AD ( H thuộc BD). Kẻ MK // BC (K thuộc AC).KE dường thẳng đi qua H và vuông góc với MH.Đường thẳng đi qua K và vuông góc với MK .Hai đường thẳng đó cắt nhau tại I.Chứng minh
MÌNH MỚI HỌC ĐƯỜNG TRUNG BÌNH CỦA HÌNH THANG VÀ TAM GIÁC . GIÚP MÌNH NHÉ !![]()
Cho hình thang ABCD có AB song song với CD, gọi E,F lần lượt là trung điểm của AD và BC phân giác của góc A và góc B cắt EF theo thứ tự ở I và K. chứng minh :
a)cm:tam giác AIK và tam giác BKF cân
b)tam giác AID và tam giác BKC
c)IE=1/2AD;KF=1/2KC
d)cho AB=5cm , CD = 18cm, AD=6cm,BC=7cm.Tính IK
Cho hình thang cân ABCD có AB//CD và AB>CD, AC ΩBD tại O. Gọi I,E,F lần lượt là trung điểm của OD,OA,BC. Chứng minh tam giác IEF đều biết góc OAB = 60 độ