- Nếu H nằm ở nửa dưới đoạn SO thì \(R\ge\dfrac{SO}{2}=\dfrac{3}{2}\)
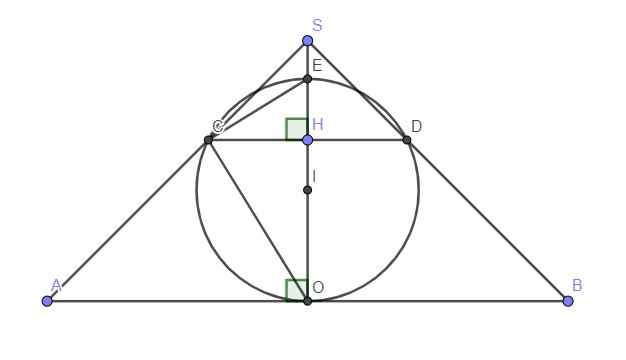
- Nếu H nằm ở nửa trên đoạn SO, thực hiện mặt cắt qua trục nón như hình vẽ
\(SO=OA=3\Rightarrow SOA\) vuông cân \(\Rightarrow SCH\) vuông cân
\(\Rightarrow CH=SH=3-OH=3-\left(R+IH\right)=3-R-\sqrt{R^2-CH^2}\)
\(\Rightarrow3-R=CH+\sqrt{R^2-CH^2}\le\sqrt{2\left(CH^2+R^2-CH^2\right)}=R\sqrt{2}\)
\(\Rightarrow R\left(\sqrt{2}+1\right)\ge3\Rightarrow R\ge\dfrac{3}{\sqrt{2}+1}=3\left(\sqrt{2}-1\right)\)
\(V_{min}=\dfrac{4}{3}\pi R_{min}^3=8,037\)