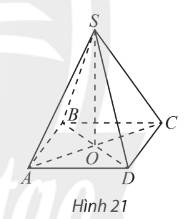
a) \(\Delta ABC\) vuông cân tại \(B \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(CC' = AA' = 2a\)
\(CC' \bot \left( {ABCD} \right) \Rightarrow CC' \bot AC\)
\( \Rightarrow \Delta ACC'\) vuông tại \(C \Rightarrow AC' = \sqrt {A{C^2} + CC{'^2}} = a\sqrt 6 \)
b) \({S_{ABC{\rm{D}}}} = {S_{A'B'C'C'}} = \frac{1}{2}\left( {A{\rm{D}} + BC} \right).AB = \frac{{3{a^2}}}{2}\)
Gọi \(M\) là trung điểm của \(AD\)
\( \Rightarrow ABCM\) là hình vuông\( \Rightarrow MC = M{\rm{D}} = MA = \frac{1}{2}A{\rm{D}} = a\)
\(\Delta MC{\rm{D}}\) vuông cân tại \(M \Rightarrow C{\rm{D}} = \sqrt {C{M^2} + D{M^2}} = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABB'A'}} = AB.AA' = 2{a^2}\\{S_{ADD'A'}} = AD.AA' = 4{a^2}\\{S_{BCC'B'}} = BC.CC' = 2{a^2}\\{S_{C{\rm{DD}}'{\rm{C}}'}} = C{\rm{D}}.CC' = 2{a^2}\sqrt 2 \end{array}\)
Tổng diện tích các mặt của hình lăng trụ là:
\(\begin{array}{l}S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'C'}} + {S_{ABB'A'}} + {S_{ADD'A'}} + {S_{BCC'B'}} + {S_{C{\rm{DD}}'{\rm{C}}'}}\\ & = \frac{{3{a^2}}}{2} + \frac{{3{a^2}}}{2} + 2{a^2} + 4{a^2} + 2{a^2} + 2{a^2}\sqrt 2 = \left( {11 + 2\sqrt 2 } \right){a^2}\end{array}\)