Question

Cho hình  chữ nhật ABCD.Gọi M là trung điểm của AB.Kẻ MN vuông gốc với CD tại N.

a) c/m AMND là hình chữ nhật

b) O là trung điểm của MN .C/m O cũng là trung điểm của AC

c) Gọi E,N lần lượt là giao điểm của AN và CM với BD chứng minh 

DE=EF=FB

Answer 1

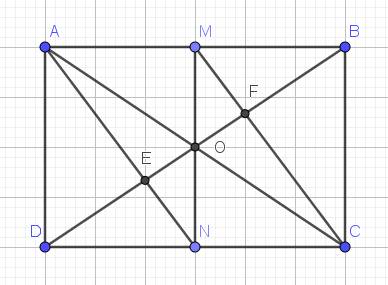
Lời giải:
a. Vì $ABCD$ là hình chữ nhật nên $\widehat{A}=\widehat{D}=90^0$

$MN\perp CD$ nên $\widehat{MND}=90^0$
Tứ giác $AMND$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{N}$ nên là hcn.

b. 

Hoàn toàn tương tự phần a ta thấy $\widheat{B}=\widehat{C}=\widehat{N}$ nên $BMNC$ là hcn

$\Rightarrow BM=NC$
$AMND$ là hcn nên $AM=DN$

Mà $AM=BM$ nên $AM=NC$
Có $AM\parallel NC$ (do $AB\parallel CD$) và $AM=NC$ nên $AMCN$ là hbh

$\Rightarrow AC, MN$ cắt nhau tại trung điểm mỗi đường.

Mà $O$ là trung điểm $MN$ nên $O$ cũng là trung điểm $AC$.

c.

Vì $AMCN$ là hbh (theo phần b) nên $AN\parallel CM$

$\Rightarrow EN\parallel FC$
$\Rightarrow \frac{DE}{EF}=\frac{DN}{NC}=1$ (theo định lý Talet)

$\Rightarrow DE=EF(1)$

Mặt khác:

$AN\parallel CM$

$\Rightarrow MF\parallel AE$

$\Rightarrow \frac{BF}{EF}=\frac{BM}{MA}=1$ (định lý Talet)

$\Rightarrow BF=EF(2)$

Từ $(1); (2)\Rightarrow DE=EF=BF$

Answer 2

Hình vẽ: