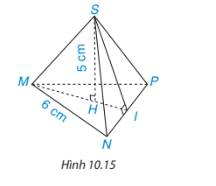
Vì tam giác MNP đều
=> MN=NP=MP=6cm
=> IN=IP=3cm
Xét tam giác MIN vuông tại I, có:
\(\begin{array}{l}M{I^2} = M{N^2} - I{N^2} = {6^2} - {3^2}\\ \Rightarrow MI = 5,2\\ \Rightarrow {S_{MNP}} = \frac{1}{2}.MI.NP = \frac{1}{2}.5,2.6 = 15,6(c{m^2})\\ \Rightarrow V = \frac{1}{3}.S.h = \frac{1}{2}.15,6.5 = 26(c{m^3})\end{array}\)
a: \(S_{MNP}=6^2\cdot\dfrac{\sqrt{3}}{4}=9\sqrt{3}\left(cm^2\right)\)
b: \(V=\dfrac{1}{3}\cdot S_{MNP}\cdot h=\dfrac{1}{3}\cdot5.19\cdot9\sqrt{3}\simeq26\left(cm^2\right)\)