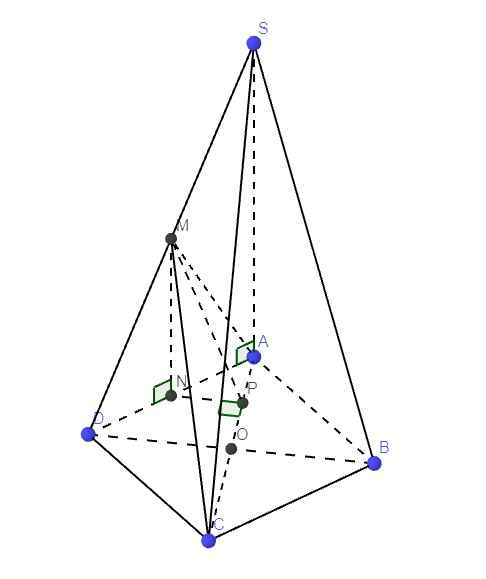
Gọi O là tâm đáy \(\Rightarrow OD\perp AC\) (đường chéo hình vuông)
Gọi N là trung điểm AD \(\Rightarrow\) MN là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}SA=\dfrac{a\sqrt{5}}{2}\\MN||SA\end{matrix}\right.\)
Do \(SA\perp\left(ABCD\right)\Rightarrow MN\perp\left(ABCD\right)\Rightarrow MN\perp AC\)
Gọi P là trung điểm AO \(\Rightarrow\) NP là đường trung bình tam giác OAD
\(\Rightarrow\left\{{}\begin{matrix}NP=\dfrac{1}{2}OD=\dfrac{a\sqrt[]{2}}{4}\\NP||OD\end{matrix}\right.\)
Mà \(OD\perp AC\Rightarrow NP\perp AC\)
\(\Rightarrow AC\perp\left(MNP\right)\)
Lại có AC là giao tuyến (AMC) và (ABCD)
\(\Rightarrow\widehat{MPN}\) là góc giữa (AMC) và (ABCD)
\(tan\widehat{MPN}=\dfrac{MN}{NP}=\sqrt{10}\Rightarrow\widehat{MPN}\approx72^027'\)