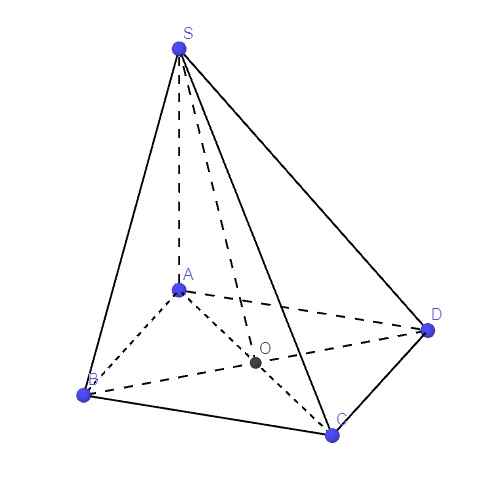
Gọi O là giao điểm AC và BD
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(\Rightarrow BO\perp\left(SAC\right)\) \(\Rightarrow SO\) là hình chiếu vuông góc của SB lên (SAC)
\(\Rightarrow\widehat{BSO}\) là góc giữa SB và (SAC)
\(OB=\dfrac{1}{2}BD=\dfrac{1}{2}.a\sqrt{2}.\sqrt{2}=a\)
\(\Rightarrow sin\widehat{BSO}=\dfrac{OB}{SB}=\dfrac{a}{2a}=\dfrac{1}{2}\)
\(\Rightarrow\widehat{BSO}=30^0\)